rocket travel escape velocity

• Science Notes Posts
• Contact Science Notes
• Todd Helmenstine Biography
• Anne Helmenstine Biography
• Free Printable Periodic Tables (PDF and PNG)
• Periodic Table Wallpapers
• Interactive Periodic Table
• Periodic Table Posters
• How to Grow Crystals
• Chemistry Projects
• Fire and Flames Projects
• Holiday Science
• Chemistry Problems With Answers
• Physics Problems
• Unit Conversion Example Problems
• Chemistry Worksheets
• Biology Worksheets
• Periodic Table Worksheets
• Physical Science Worksheets
• Science Lab Worksheets
• My Amazon Books

Escape Velocity Definition and Formula

Escape velocity is a fundamental concept in astrophysics and aerospace engineering, crucial for understanding the mechanics of space travel and celestial mechanics. Here is the definition of escape velocity, its nature as a speed rather than a velocity, its applications, the formula governing it, and a table of values for various celestial bodies.

What Is Escape Velocity?

Escape velocity is the minimum speed an object must reach to break free from the gravitational pull of a body without further propulsion. This means that a spacecraft, for instance, must attain this speed to escape the Earth’s gravitational field without needing additional energy input, such as from rockets.

Speed vs. Velocity: Why Escape Velocity Is a Speed

While often referred to as a “velocity,” escape velocity is technically a scalar quantity , which means it has magnitude but no specific direction. In contrast, “velocity” is a vector quantity, encompassing both magnitude and direction. Therefore, the term “escape speed” is more accurate. What matters in overcoming a body’s gravitational pull is the object’s speed (how fast it’s moving), not the direction of its movement.

Uses and Applications

Knowing the escape velocity of a body has several applications:

• Space Travel : The most direct application is in determining the initial speed required for spacecraft to leave a planet or moon.
• Astrophysics : Knowing the escape speed helps in understanding the behavior of celestial objects, like the conditions necessary for an atmosphere to remain bound to a planet.
• Planetary Science : The calculation assists in studying the gravitational fields of planets and moons, which is crucial for landing and takeoff of space missions.

The Escape Velocity Formula

The formula for escape velocity derives from the law of conservation of energy :

v e ​ = (2 GM /r​​) 1/2

• v e ​ is the escape velocity.
• G is the gravitational constant (6.674×10−11 Nm 2 /kg 2 ).
• M is the mass of the celestial body.
• r is the radius of the celestial body from its center to the point of escape

Escape Velocity for Earth

For Earth, the values are:

• M Earth ​= 5.972×10 24 kg
• r Earth ​ = 6.371×10 6 m

Plugging in the values and performing the calculation:

v e ​= (2 × 6.674×10 −11 Nm 2 /kg 2 × 5.972×10 24 kg ​​/ 6.371×10 6 m) 1/2

Remember, 1 N = 1 kg⋅m/s 2

So, the escape velocity for Earth is approximately 11,185.7311,185.73 meters per second or 11.2 m/s.

Escape Velocity Table for Celestial Bodies

This table provides the mass, radius, and calculated escape velocity for various celestial bodies, including the Sun, Mercury, Venus, Earth, Moon, Mars, Jupiter, Saturn, Uranus, Neptune, and Pluto.

The escape velocity of the Milky Way galaxy is between 492 and 594 km/s. Meanwhile, the intense gravitational pull of a black hole is so high that its escape velocity is faster than the speed of light !

Deriving the Formula for Escape Velocity

The escape velocity formula comes from the principle of conservation of energy, based on two states of the system: one when the object is at the surface of the celestial body (like a planet) and the other when the object is at an infinite distance away, having just escaped the gravitational pull of the body.

Object on the Surface

At this state, the object at the surface has the following energies:

• Gravitational Potential Energy (U) : U 1 ​ = − GMm / r​
• Kinetic Energy (K) : K 1 ​ = 1/2 mv 2 (where v is the velocity of the object)

The total energy at state 1 (E1) is the sum of kinetic and potential energy:

E 1 ​= K 1​ + U 1 ​= 1/2​ mv 2 − GMm / r ​

Object at an Infinite Distance

At infinite distance, the gravitational potential energy becomes zero because the object is no longer within the gravitational influence of the celestial body. Also, for the object to just escape, we assume its kinetic energy reduces to zero (i.e., it escapes but eventually comes to rest). So:

• Gravitational Potential Energy (U) : U 2 ​ = 0
• Kinetic Energy (K) : K 2 ​=0

Therefore, the total energy at state 2 (E 2 ) is: E 2 ​= K 2 ​+ U 2 ​ = 0

Conservation of Energy

According to the law of conservation of energy, the total mechanical energy of the system remains constant if only conservative forces (like gravity) are doing work. Therefore, E 1 ​ = E 2 ​.

Setting the total energies equal to each other: 1/2​ mv 2 − GMm ​ /r = 0

Solving for Escape Velocity

Now, we solve for v , the escape velocity:

1/2 mv 2 = GMm / r ​

mv 2 = 2 GMm / r

v 2 = 2 GM / r

v = (2 GM / r ) 1/2 ​​​​

Here, G is the gravitational constant, M is the mass of the celestial body, m is the mass of the object, and r is the distance from the center of the celestial body to the object (typically the radius of the body). Mass cancels out, showing that escape velocity is independent of the mass of the escaping object.

Why Launches Are Close to the Equator

Rockets achieve escape velocity (or orbital velocity, if the goal is to orbit rather than escape) through sustained acceleration. They do not need to reach escape velocity instantly; instead, they gradually increase their speed over time using their engines. Launching spacecraft close to the equator takes advantage of the Earth’s rotation, giving the craft a boost toward achieving escape velocity and offering additional advantages:

1. Rotational Speed of the Earth

The Earth rotates faster at the equator than at any other latitude . This means that a location on the equator is moving eastward at a higher speed compared to locations further north or south. When a spacecraft launches from the equator, it benefits from this additional rotational speed of the Earth. The extra speed provided by the Earth’s rotation means the rocket requires less fuel to reach the necessary orbital velocity, making the launch more efficient. Also, although the effect is minor, planets are slightly flattened, so the equator is slightly further from the center of the planet than the poles.

3. Direct Access to Geostationary Orbit

Geostationary orbits are directly above the equator. Launching from the equator allows for a more direct and fuel-efficient path to this type of orbit, which is important for communication and weather satellites.

4. Flexibility in Launch Azimuth

Launching from near the equator offers more flexibility in choosing a launch azimuth (the angle of the launch relative to North). This flexibility is crucial for efficiently reaching different types of orbits, especially equatorial and geostationary orbits.

5. Energy Efficiency

The rotational boost and the direct path to certain orbits mean that rockets can carry more payload for the same amount of fuel, or the same payload with less fuel. This efficiency is crucial for cost-effective space missions.

• Bate, Roger R.; Mueller, Donald D.; White, Jerry E. (1971). Fundamentals of Astrodynamics (Illustrated ed.). Courier Corporation. ISBN 978-0-486-60061-1.
• Giancoli, Douglas C. (2008). Physics for Scientists and Engineers with Modern Physics . Addison-Wesley. ISBN 978-0-13-149508-1.
• Smith, Martin C.; Ruchti, G. R.; Helmi, A.; Wyse, R. F. G. (2007). “The RAVE Survey: Constraining the Local Galactic Escape Speed”. Proceedings of the International Astronomical Union . 2 (S235): 755–772. doi: 10.1017/S1743921306005692
• Teodorescu, P. P. (2007). Mechanical Systems, Classical Models . Springer, Japan. ISBN 978-1-4020-5441-9.

Related Posts

A Remarkable New Thruster Could Achieve Escape Velocity—and Interplanetary Travel

Scientists are on the brink of a propulsion breakthrough.

• Ion thrusters are the most common primary engine powering satellites through orbital maneuvers today.
• But to travel from low-Earth orbit (LEO) to farther orbits—or even the Moon—requires a different kind of ion thruster capable of achieving escape velocity and orbital capture maneuvers.
• Using technology originally developed for NASA’s upcoming lunar space station, the space agency has miniaturized its high-power solar electric tech into an engine that could make more complex satellites and planetary missions possible.

These engines are as old as rocketry itself— Soviet and German rocket leaders first dreamed up their future uses more than a century ago. And today, these electric propulsion systems power the swarms of satellites around Earth that make modern life possible. Unlike chemical rockets that throw out gasses for propulsion, ion engines are powered by individual atoms , which makes them much more fuel efficient and allows satellites to operate for longer.

However, they’re not perfect. In the future, spacecraft will need to perform high-velocity propulsive maneuvers—such as achieving escape velocity and orbital capture—that current ion engines can’t deliver. That’s why NASA developed the H71M sub-kilowatt Hall-effect thruster , a next-generation ion engine that can supply a velocity change.

The propulsion system must operate using low power (sub-kilowatt) and have high-propellant throughput (i.e., the capability to use a high total mass of propellant over its lifetime) to enable the impulse required to execute these maneuvers. While commercial ion thrusters are good enough for most LEO satellites , these engines only use “10% or less of a small spacecraft’s initial mass in propellant,” according to NASA. The H71M thruster uses 30 percent, and could operate for 15,000 hours.

“Small spacecraft using the NASA-H71M electric propulsion technology will be able to independently maneuver from low-Earth orbit (LEO) to the Moon or even from a geosynchronous transfer orbit (GTO) to Mars,” NASA wrote on its website regarding the new ion thruster. “The ability to conduct missions that originate from these near-Earth orbits can greatly increase the cadence and lower the cost of lunar and Mars science missions.”

The creation of this thruster grew from NASA’s work on the Power and Propulsion Element for Gateway , NASA’s planned lunar orbital space station. The team essentially miniaturized the high-power solar electric technologies that will make that lunar mission possible into a package that could provide thrust for smaller space missions.

One of the first spacecraft companies that will use this next-gen technology is SpaceLogistics, a space subsidiary of Northrop Grumman. The company’s NGHT-1X Hall-effect thrusters are based on NASA’s technology, and will allow its Mission Extension Pod (MEP)—which, as its name suggests, is essentially a satellite repair vehicle—to reach geosynchronous Earth orbit, where it’ll attach itself to a larger satellite. Acting as a “propulsion jet pack,” the MEP will act as an ion-powered symbiote that extends the larger satellite’s mission by at least six years.

If all goes well, this small-yet-mighty thruster could enable planetary missions once considered impossible to pull off.

Darren lives in Portland, has a cat, and writes/edits about sci-fi and how our world works. You can find his previous stuff at Gizmodo and Paste if you look hard enough. 

.css-cuqpxl:before{padding-right:0.3125rem;content:'//';display:inline;} Rockets .css-xtujxj:before{padding-left:0.3125rem;content:'//';display:inline;}

An Engineer Says He’s Overcome Earth’s Gravity

Scientists Get Serious in Search for Warp Drive

A Chinese Rocket Took an Unknown Item to the Moon

The Pentagon Really Wants a Nuclear Spacecraft

Cylinder on Australian Beach is Part of a Rocket

Why the Aerospike Engine Is the Future of Rockets

After 70 Years, Will Aerospike Engines Fly?

Is Fusion the Future of Space Exploration?

Astronauts Might be Able to Hibernate in 10 Years

SpaceX Blew Up Their Own Launch Pad

Welp, SpaceX’s Starship Just Blew Up

Escape Velocity

Artist’s conception of NASA’s Space Launch System (NASA).

How does this align with my curriculum?

Share on: facebook x/twitter linkedin pinterest.

Why do a baseball and a rocket need the same launch speed to get from Earth into space? It has to do with physics and gravitational force.

In early 2018, Elon Musk made headlines by launching his Tesla Roadster into space , playing David Bowie’s “Starman” on repeat as it made its slow journey through space. This was a fun publicity stunt. But how the Roadster got to space is an even cooler story.

The Roadster hitched a ride on the newest SpaceX rocket, the Falcon Heavy , as it made its maiden voyage into space. At the time of its launch, the Falcon Heavy was the most powerful operational rocket in the world (though not in history).

Did you know? The Falcon Heavy weighs almost 1.5 million kilograms! 

How do you launch something into space?

You might be wondering about how hard it is to launch something that large. How fast does it need to go? Surprisingly, getting anything into deep space (beyond the Earth’s orbit) from the surface of the Earth—the Falcon Heavy, a Roadster, or even a baseball—requires the same launch speed. This speed is called escape velocity , since it’s just enough speed to escape the gravitational pull of the Earth. 

But why is the escape velocity the same, no matter the mass of the object? The reason is that mass and escape velocity are not related. For example, say you wanted to drive 100 km in an hour. It would not matter if you were driving a tiny car or a big transport truck. You would still need to drive at a speed of 100 km/h to reach this goal.

So what exactly is the escape velocity from the surface of the Earth? It is a whopping 11.2 km/s (kilometres per second). That’s more than 40 000 km/h. At that speed, you could travel from the North Pole to the South Pole in about 21 minutes!

Misconception Alert Going into Space vs. Escape Velocity Most satellites and spacecraft sent into space do not reach escape velocity! Space is usually considered to start at an altitude of 100 km (this is known as the Kármán line). If a rocket goes fast enough and high enough to enter space but does not reach escape velocity, it will enter orbit around the Earth. The International Space Station and many satellites orbit the Earth.

How do you calculate escape velocity?

Escape velocity depends on a number of factors. Let’s take a step back for a moment. Scientists have determined that the escape velocity for any large object (such as a planet or star) can be calculated from the following equation:

ve = √(2GM/r)

The M in the equation represents the mass of the planet. Planets with more mass are harder to escape than planets with less mass. This is because the more mass a planet has, the stronger its force of gravity. For example, when you watch footage of astronauts jumping on the Moon, it looks effortless. This is because the Moon’s mass (and therefore its gravity) is much less than Earth’s. 

The r in the equation represents radius , which is the distance between the centre of the planet and the object that is trying to escape. In other words, radius is the distance between the centre of the planet and its surface. As an object moves away from the planet, the planet’s gravitational pull will have less of an influence on it. If the object moves far enough away, it feels almost no attraction. When this happens, the escape velocity will basically be zero! 

Finally, the G in the equation is a constant. Specifically, it is Newton’s universal constant of gravity . For the moment, all you need to know is that we need this constant to make the equation work. G is approximately equal to 6.67 × 10 –11 metres 3 /(kg)(second) 2 .

Now, let’s plug in some numbers to determine the escape velocity from the surface of the Earth. For M, we use the mass of the Earth, which is approximately 5.97 × 10 24 kg.

For r, since we are calculating the escape velocity from the surface of the Earth, we can use the Earth’s radius, which is approximately 6.37 × 10 6 m.

We can now calculate the escape velocity for the Earth:

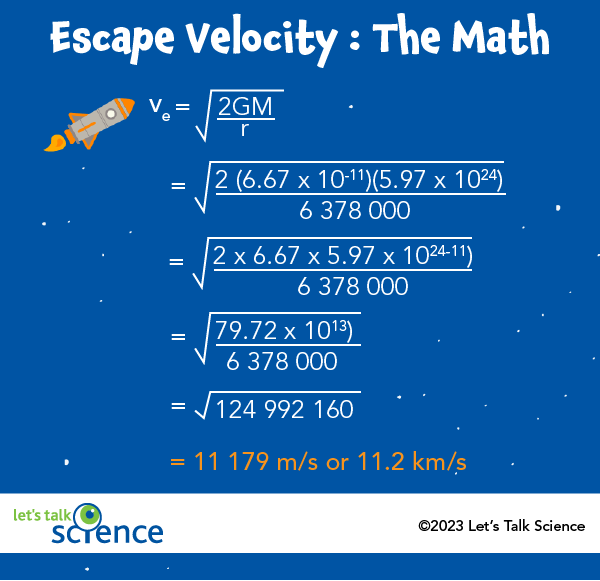
Escape velocity equals the square roots of 2GM over r which equals the square root of 2 times 6.67 times ten to the minus eleven times 5.97 times ten to the twenty fourth over 6 378 000, which equals approximately 11.2 kilometers per second.

You can calculate the escape velocity from any body in space as long as you know its radius and its mass. For example, using the above equation, we can calculate the escape velocity of the Moon. From its equator, the Moon has a radius of 1 738 km. It also has an estimated mass of 7.342 × 10 22 kg. This means that the Moon’s escape velocity is 2.38 km/s. That is much less than the 11.2 km/s it takes to get off the Earth. In the future, perhaps rockets will be built on and take off from the Moon rather than from Earth!

The escape velocity of Mars is 4.25 km.s. The escape velocity of Earth is 11.19 km/s. The escape velocity of Venus is 10.36 km/s. The escape velocity of Mars is 5.03 km/s. The escape velocity of Saturn is 36.09 km/s. The escape velocity of Uranus is 21.38 km/s. The escape velocity of Neptune is 23.56 km/s. The escape velocity of Jupiter is 60.20 km/s.

Did you know? As of 2019, only 24 humans have ever reached escape velocity. They were the crews of the Apollo missions that flew to the Moon between 1968 and 1972.

We’ve taken a first glimpse at the rocket science needed to get the Falcon Heavy (and a Roadster playing David Bowie) into space. All we need to do is accelerate the rocket to 11.2 km/s and point it upwards. As the scientists and engineers at SpaceX know well, acceleration and pointing the rockets are the hard part! 

Starting Points

Connecting and relating.

• Have you watched a rocket launch before? Have you heard the launch team talk about boosters firing and boosters falling away? What do you think is the purpose of boosters? 
• If you could launch something into space, what would you choose? Why?

Relating Science and Technology to Society and the Environment

• What would be the advantage, from an escape velocity perspective, of sending spacecraft to Mars from the Moon or a space station?
• What are the advantages and disadvantages of reusable rocket boosters like the Falcon Heavy compared to older rockets like the Saturn V for sending spacecraft beyond Earth orbit?
• What would the advantages and disadvantages of launching spacecraft to the Moon or Mars from low Earth orbit (e.g., from the International Space Station) vs. from the surface of the Earth? Would the benefits outweigh the costs?

Exploring Concepts

• What is escape velocity? Is escape velocity actually a velocity? Explain.
• How does the size of planetary body impact on its escape velocity?
• Does there come a point where a mass is too large to get off the Earth? Explain.

Nature of Science/Nature of Technology

Is the cost and risk of sending spacecraft beyond Earth orbit justified by the scientific gains?

Media Literacy

• What media you seen heard or read about the Falcon Heavy? What types of media were used by SpaceX to promote the lift-off event? What audiences is the company targeting? How does the media from SpaceX differ from the media produced by NASA? 
• Does a media stunt such as launching a car into space help raise awareness of and support of space exploration?

Teaching Suggestions

• This article and embedded video can be use for Physics and Space Science teaching and learning related to planetary science. Concepts introduced include rocket, escape velocity, mass (M), radius (r), center, distance and Newton’s universal constant of gravity (G). 
• After reading this article, teachers could have students consolidate their understanding of escape velocity using a Concept Definition Web learning strategy. Ready-to-use Concept Definition Web reproducibles are available in [ Google doc ] and [ PDF ] formats.
• For a math and physics focus and follow-up to reading this article, teachers could have students calculate the escape velocity for the other planets, given their mass and radius measurements. Their answers could be checked using the graphic in the article titled Escape Velocities from Planets in our Solar System.

Living Space

Explore the optimal environmental conditions for human life. How do you think your classroom conditions compare to those on the International Space Station? Free project for grades 6-9 students.

Falcon Heavy

Fact sheet from SpaceX on the Falcon Heavy rocket; includes, infographics, stats, and videos. A Year After SpaceX’s 1st Falcon Heavy Launch, Starman (and a Tesla) Sail On (2019)

Article by Mike Wall exploring the status of the Tesla that was launched into space with the Falcon Heavy.

Barnett, A., & Wattles, J. (2018). SpaceX Falcon Heavy: How it stacks up with other massive rockets . CNN.

The Editors of Encyclopaedia Britannica. (2016). Escape velocity .

Grayzeck, E. (2017). Moon fact sheet . NASA.

Softschools.com. (n.d.) Escape velocity formula .

Space Exploration Technologies Corp.(2018). Falcon Heavy technical overview .

Steemit. (2018). Escape velocities: Launching satellites into space .

Williams, D. (2019). Earth fact sheet . NASA.

Williams, D. (2017). Planetary fact sheet. NASA.

Related Topics

• Random article
• Teaching guide
• Privacy & cookies

Space rockets

by Chris Woodford . Last updated: September 28, 2023.

Photo: Looking up at the base of a Saturn V rocket like the ones that put astronauts on the Moon in the 1960s. The five red things are the five engines of the lowest rocket stage (technically called S-IC). Picture courtesy of NASA .

Photo: Space as we know it. Photo of stellar swarm M80 (NGC 6093), a dense star cluster in the Milky Way galaxy, taken by the Hubble Space Telescope and courtesy of NASA on the Commons .

Where does space start?

What is space like, is there more than one kind of space, how do rockets work.

Photo: An Atlas Centaur rocket launches a scientific satellite in 1990. Picture courtesy of NASA Marshall Space Flight Center (NASA-MSFC) .

Photo: Action and reaction: rockets work by firing jets of hot gas downward (the action), which makes them move upward (the reaction). The gas isn't pushing against anything to make the rocket move: the very act of the gas shooting back moves the rocket forward—and that can happen in "empty" space just as well as inside Earth's atmosphere. This picture shows Space Shuttle mission STS-26 in 1988, when the Shuttle made its brave and confident return to space after the Challenger disaster two years earlier. Photo courtesy of NASA on the Commons .

Thrust and drag

Artwork: Forces acting on a plane (left) and a rocket (right). When a plane flies at steady speed, the forward thrust made by the engines is equal to the air resistance (drag) pulling back. The upward force of lift created by the wings is equal to the downward force of the plane's weight. In other words, the two pairs of forces are in perfect balance. With a rocket, thrust from the engines pushes upward while weight and drag try to pull it back down. When the rocket accelerates upward, the thrust is greater than the combined lift and drag. The various surfaces of a rocket can also produce lift, just like the wings of a plane, but it acts sideways instead of upwards. Although this sounds confusing, it's easy to see why if you imagine the blue plane rotated through 90 degrees so it's flying straight up like a rocket: the lift would also be pointing sideways.

Escape velocity

Artwork: Little pieces of history: An interesting cutaway showing the main component parts of the now-retired Space Shuttle orbiter. Picture courtesy of NASA Marshall Space Flight Center (NASA-MSFC) . Browse the hi-resolution version of this image (via Wikimedia Commons).

Photo: Test firing the Space Shuttle's main engine. Picture courtesy of NASA on the Commons .

Artwork: How a space rocket works—greatly simplified: Unlike airplane jet engines , which take in air as they fly through the sky, space rockets have to carry their own oxygen supplies ( oxidizers ) with them because there is no air in space. Liquid hydrogen (the fuel) from one tank is mixed with liquid oxygen (the oxidizer) from a separate tank using pumps and valves to control the flow. The oxidizer and fuel mix and burn in the combustion chamber, making a hot blast of exhaust gas that propels the rocket. The payload (the cargo—such as a satellite) occupies a relatively small proportion of the rocket's total volume in the nose-cone at the top.

Photo: An Ariane 5 rocket waiting to launch the James Webb Space Telescope . Picture by Chris Gunn courtesy of NASA and Wikimedia Commons .

Key parts of an Ariane rocket

Artwork: The parts of an Ariane 5 rocket. The central rocket comprises two stages: the lower Cryogenic Main Stage (EPC, orange dotted line) and the Cryogenic Upper Stage (ESC-A, gray dotted line). Solid rocket boosters (orange) stand on each side. Inside the central rocket, the main parts are: 1) Detachable fairing to protect payload as the rocket blasts through Earth's atmosphere; 2) Payload consisting of (in this mission) two satellites to be launched; 3) Satellite mounted on top is launched last; 4) Speltra structure allows two satellites to be launched in the same mission; 5) Satellite mounted underneath Speltra is launched first; 6) Small Aestus engine; 7) Liquid oxygen tank; 8) Liquid hydrogen tank; 9) Vulcain main engine.

A closer look at a scientific rocket

Artwork: Early design for a high-altitude rocket camera from US Patent: 1,102,653: Rocket Apparatus by Robert Hutchings Goddard, July 7, 1914, courtesy of US Patent and Trademark Office (with some details removed and colors added for ease of explanation).

Photo: The father of modern rocketry, Robert Hutchings Goddard, pictured in November 1925 with one of his inventions , the double-acting rocket engine. Goddard first got the idea of traveling into space as a teenager, after climbing a cherry tree in his family's garden: "I imagined how wonderful it would be to make some device which had even the possibility of ascending to Mars..." His many inventions included powering rockets with liquid fuels and constructing rockets with multiple stages—two fundamentally important ideas used in virtually every successful space rocket launched to date. Picture courtesy of NASA on the Commons .

Photo: An early Atlas rocket photographed in 1963. Picture courtesy of NASA on the Commons .

Photo: A SpaceX Falcon 9 rocket being launched in 2020. Picture courtesy of NASA on the Commons .

Photo: The Space Launch System (SLS) under construction in the vast Vehicle Assembly Building at NASA’s Kennedy Space Center in Florida. Picture courtesy of NASA Image and Video Library .

If you liked this article...

Find out more, on this website.

• History of flight
• Jet engines (airplane engines)
• Forces and motion

On other websites

• NASA and European Space Agency : What's the latest news from the world of space exploration?
• The Space Educators Handbook : A superb collection of educational resources compiled by NASA's Jerry Woodfill.
• Rockets: A Teacher's Guide with Activities in Science, Mathematics, and Technology : A comprehensive 100-page guide to rocketry for K-12 educators and their students.
• Smithsonian National Air and Space Museum : A great place to learn how people conquered flight.
• Space.com : One of the web's most popular space news sites.

For older readers

• Apollo 11: The Inside Story by David Whitehouse. Icon, 2019. On the 50th anniversay of the Apollo moon landing, this book takes a new look at one of the most inspiring scientific success stories of all time.
• Rocket: Owners' Workshop Manual: 1942 Onwards by David Baker. Haynes, 2015. Some great cutaways accompanied by lavish photos. This book covers both the general principles of how rockets work and examples of classic rockets from the last half century.
• Eyewitness: Space Exploration by Carole Stott et al. DK, 2014. What's out there, beyond the sky, in the darkness where we can only imagine? A colorful introduction from Dorling Kindersley.
• Man on the Moon by Andrew Chaikin. Penguin, 2010. An engaging read that charts the historic Apollo missions and the men who made them possible.

For younger readers

• Space Encyclopedia: A Tour of Our Solar System and Beyond by David A. Aguilar et al, National Geographic, 2020. This one's suitable for ages 9–12.
• Eyewonder: Space by Carole Stott. DK, 2016. A short (56-page) introduction for ages 5–9.
• Space: Smithsonian by Robert Dinwiddie et al. DK, 2015. An information-packed but visually very engaging introduction for ages 9–12.
• Fueling up and Heading out by Neil deGrasse Tyson, Natural History Magazine, June, 2005. These two engaging essays explain how a rocket gets off the ground and how it moves around in space once it gets there.

Text copyright © Chris Woodford 2006, 2022. All rights reserved. Full copyright notice and terms of use .

Rate this page

Tell your friends, cite this page, more to explore on our website....

• Get the book
• Send feedback

Chapter 4: Trajectories

Chapter objectives.

Upon completion of this chapter you will be able to describe the use of Hohmann transfer orbits in general terms and how spacecraft use them for interplanetary travel. You will be able to describe the general concept of exchanging angular momentum between planets and spacecraft to achieve gravity assist trajectories.

When traveling among the planets, it's a good idea to minimize the propellant mass needed by your spacecraft and its launch vehicle. That way, such a flight is possible with current launch capabilities, and costs will not be prohibitive.

The amount of propellant needed depends largely on what route you choose. Trajectories that by their nature need a minimum of propellant are therefore of great interest.

Hohmann Transfer Orbits

To launch a spacecraft from Earth to an outer planet such as Mars using the least propellant possible, first consider that the spacecraft is already in solar orbit as it sits on the launch pad. This existing solar orbit must be adjusted to cause it to take the spacecraft to Mars: The desired orbit's perihelion (closest approach to the Sun) will be at the distance of Earth's orbit, and the aphelion (farthest distance from the Sun) will be at the distance of Mars' orbit. This is called a Hohmann Transfer orbit. The portion of the solar orbit that takes the spacecraft from Earth to Mars is called its trajectory .

From the previous chapter, we know that the task is to increase the apoapsis (aphelion) of the spacecraft's present solar orbit. Recall from Chapter 3...

A spacecraft's apoapsis altitude can be raised by increasing the spacecraft's energy at periapsis.

Well, the spacecraft is already at periapsis. So the spacecraft lifts off the launch pad, rises above Earth's atmosphere, and uses its rocket to accelerate in the direction of Earth's revolution around the Sun to the extent that the energy added here at periapsis (perihelion) will cause its new orbit to have an aphelion equal to Mars' orbit. The acceleration is tangential to the existing orbit. How much energy to add? See the Rocket & Space Technology website.

After this brief acceleration away from Earth, the spacecraft has achieved its new orbit, and it simply coasts the rest of the way. The launch phase is covered further in Chapter 14.

Earth to Mars via Least Energy Orbit

Getting to the planet Mars, rather than just to its orbit, requires that the spacecraft be inserted into its interplanetary trajectory at the correct time so it will arrive at the Martian orbit when Mars will be there. This task might be compared to throwing a dart at a moving target. You have to lead the aim point by just the right amount to hit the target. The opportunity to launch a spacecraft on a minimum-energy transfer orbit to Mars occurs about every 25 months.

To be captured into a Martian orbit, the spacecraft must then decelerate relative to Mars using an orbit insertion rocket burn or some other means. To land on Mars from orbit, as did Viking, the spacecraft must decelerate even further using a rocket burn to the extent that the lowest point of its Martian orbit will intercept the surface of Mars. Since Mars has an atmosphere, final deceleration may also be performed by aerodynamic braking direct from the interplanetary trajectory, and/or a parachute, and/or further retrograde burns.

Inward Bound

To launch a spacecraft from Earth to an inner planet such as Venus using least propellant, its existing solar orbit (as it sits on the launch pad) must be adjusted so that it will take it to Venus. In other words, the spacecraft's aphelion is already the distance of Earth's orbit, and the perihelion will be on the orbit of Venus.

This time, the task is to decrease the periapsis (perihelion) of the spacecraft's present solar orbit. Recall from Chapter 3...

A spacecraft's periapsis altitude can be lowered by decreasing the spacecraft's energy at apoapsis .

To achieve this, the spacecraft lifts off of the launch pad, rises above Earth's atmosphere, and uses its rocket to accelerate opposite the direction of Earth's revolution around the Sun, thereby decreasing its orbital energy while here at apoapsis (aphelion) to the extent that its new orbit will have a perihelion equal to the distance of Venus's orbit. Once again, the acceleration is tangential to the existing orbit.

Of course the spacecraft will continue going in the same direction as Earth orbits the Sun, but a little slower now. To get to Venus, rather than just to its orbit, again requires that the spacecraft be inserted into its interplanetary trajectory at the correct time so it will arrive at the Venusian orbit when Venus is there. Venus launch opportunities occur about every 19 months.

Type I and II Trajectories

If the interplanetary trajectory carries the spacecraft less than 180 degrees around the sun, it's called a Type-I Trajectory. If the trajectory carries it 180 degrees or more around the Sun, it's called a Type-II.

Gravity Assist Trajectories

Chapter 1 pointed out that the planets retain most of the solar system's angular momentum. This momentum can be tapped to accelerate spacecraft on so-called "gravity-assist" trajectories. It is commonly stated in the news media that spacecraft such as Voyager, Galileo, and Cassini use a planet's gravity during a flyby to slingshot it farther into space. How does this work? By using gravity to tap into the planet's tremendous angular momentum.

In a gravity-assist trajectory, angular momentum is transferred from the orbiting planet to a spacecraft approaching from behind the planet in its progress about the sun.

Experimenters and educators may be interested in the  Gravity Assist Mechanical Simulator , a device you can build and operate to gain an intuitive understanding of how gravity assist trajectories work. The linked pages include an illustrated " primer " on gravity assist.

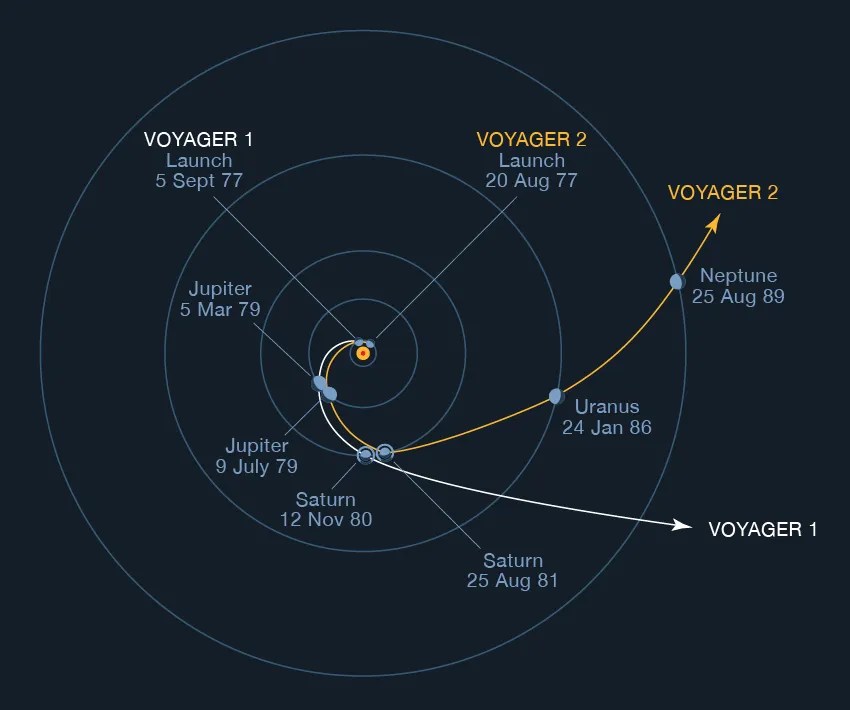
Consider Voyager 2, which toured the Jovian planets. The spacecraft was launched on a Type-II Hohmann transfer orbit to Jupiter. Had Jupiter not been there at the time of the spacecraft's arrival, the spacecraft would have fallen back toward the sun, and would have remained in elliptical orbit as long as no other forces acted upon it. Perihelion would have been at 1 au, and aphelion at Jupiter's distance of about 5 au.

However, Voyager's arrival at Jupiter was carefully timed so that it would pass behind Jupiter in its orbit around the Sun. As the spacecraft came into Jupiter's gravitational influence, it fell toward Jupiter, increasing its speed toward maximum at closest approach to Jupiter. Since all masses in the universe attract each other, Jupiter sped up the spacecraft substantially, and the spacecraft tugged on Jupiter , causing the massive planet to actually lose some of its orbital energy.

The spacecraft passed on by Jupiter since Voyager's velocity was greater than Jupiter's escape velocity, and of course it slowed down again relative to Jupiter as it climbed out of the huge gravitational field. The speed component of its Jupiter-relative velocity outbound dropped to the same as that on its inbound leg.

But relative to the Sun, it never slowed all the way to its initial Jupiter approach speed. It left the Jovian environment carrying additional orbital angular momentum stolen from Jupiter. Jupiter's gravity served to connect the spacecraft with the planet's ample reserve of angular momentum. This technique was repeated at Saturn and Uranus.

Voyager 2 Gravity Assist Velocity Changes

The same can be said of a baseball's acceleration when hit by a bat: angular momentum is transferred from the bat to the slower-moving ball. The bat is slowed down in its "orbit" about the batter, accelerating the ball greatly. The bat connects to the ball not with the force of gravity from behind as was the case with a spacecraft, but with direct mechanical force (electrical force, on the molecular scale, if you prefer) at the front of the bat in its travel about the batter, translating angular momentum from the bat into a high velocity for the ball.

(Of course in the analogy a planet has an attractive force and the bat has a repulsive force, thus Voyager must approach Jupiter from a direction opposite Jupiter's trajectory and the ball approaches the bat from the direction of the bats trajectory.)

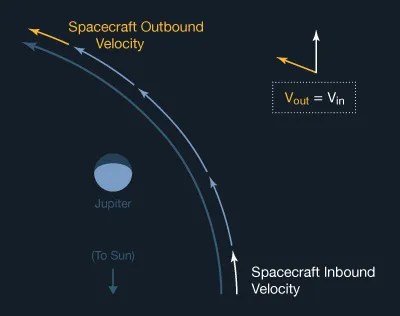
See the vector diagram showing the spacecraft's speed relative to Jupiter during a gravity-assist flyby. The spacecraft slows to the same velocity going away that it had coming in, relative to Jupiter, although its direction has changed. Note also the temporary increase in speed nearing closest approach.

When the same situation is viewed as Sun-relative in the diagram below, we see that Jupiter's Sun-relative orbital velocity is added to the spacecraft's velocity, and the spacecraft does not lose this component on its way out. Instead, the planet itself loses the energy.

The massive planet's loss is too small to be measured, but the tiny spacecraft's gain can be very great. Imagine a gnat flying into the path of a speeding freight train.

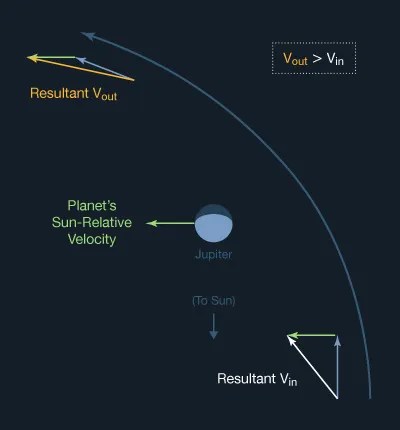
Gravity assists can be also used to decelerate a spacecraft, by flying in front of a body in its orbit, donating some of the spacecraft's angular momentum to the body. When the Galileo spacecraft arrived at Jupiter, passing close in front of Jupiter's moon Io in its orbit, Galileo lost energy in relation to Jupiter, helping it achieve Jupiter orbit insertion, reducing the propellant needed for orbit insertion by 90 kg.

The gravity assist technique was championed by Michael Minovitch in the early 1960s, while he was a UCLA graduate student working during the summers at JPL. Prior to the adoption of the gravity assist technique, it was believed that travel to the outer solar system would only be possible by developing extremely powerful launch vehicles using nuclear reactors to create tremendous thrust, and basically flying larger and larger Hohmann transfers.

An interesting fact to consider is that even though a spacecraft may double its speed as the result of a gravity assist, it feels no acceleration at all. If you were aboard Voyager 2 when it more than doubled its speed with gravity assists in the outer solar system, you would feel only a continuous sense of falling. No acceleration. This is due to the balanced tradeoff of angular momentum brokered by the planet's -- and the spacecraft's -- gravitation.

Enter the Ion Engine

All of the above discussion of interplanetary trajectories is based on the use of today's system of chemical rockets, in which a launch vehicle provides nearly all of the spacecraft's propulsive energy. A few times a year the spacecraft may fire short bursts from its chemical rocket thrusters for small adjustments in trajectory. Otherwise, the spacecraft is in free-fall, coasting all the way to its destination. Gravity assists may also provide short periods wherein the spacecraft's trajectory undergoes a change.

But ion electric propulsion, as demonstrated in interplanetary flight by Deep Space 1 -- and employed on the Dawn science mission to the asteroids -- works differently. Instead of short bursts of relatively powerful thrust, electric propulsion uses a more gentle thrust continuously over periods of months or even years. It offers a gain in efficiency of an order of magnitude over chemical propulsion for those missions of long enough duration to use the technology. Ion engines are discussed further under Propulsion in Chapter 11.

Click the image below for more information about Deep Space 1. The Japan Aerospace Exploration Agency's asteroid explorer HAYABUSA also employed an ion engine.

Even ion-electric propelled spacecraft need to launch using chemical rockets, but because of their efficiency they can be less massive, and require less powerful (and less expensive) launch vehicles. Initially, then, the trajectory of an ion-propelled craft may look like the Hohmann transfer orbit. But over long periods of continuously operating an electric engine, the trajectory will no longer be a purely ballistic arc.

Discover More Topics From NASA

Asteroids, Comets & Meteors

Kuiper Belt

Ask an Explainer

How does a rocket leave from the escape velocity in earth.

The escape velocity defines how fast a rocket needs to fly so as to escape the strength of the earth's gravitational pull. Basically, if you can go fast enough, not everything that goes up has to come down!

The trick, then, is to get enough speed. The escape velocity of earth is 11 kilometers per second (7 miles per second). On top of that, you're trying to get a thousand-ton rocket to go that speed  up into the sky . So to do this, the rocket needs to generate enough thrust to push itself into space. A tremendous feat!

Space Travel Calculator

Table of contents

Ever since the dawn of civilization, the idea of space travel has fascinated humans! Haven't we all looked up into the night sky and dreamed about space?

With the successful return of the first all-civilian crew of SpaceX's Inspiration4 mission after orbiting the Earth for three days, the dream of space travel looks more and more realistic now.

While traveling deep into space is still something out of science fiction movies like Star Trek and Star Wars, the tremendous progress made by private space companies so far seems very promising. Someday, space travel (or even interstellar travel) might be accessible to everyone!

It's never too early to start planning for a trip of a lifetime (or several lifetimes). You can also plan your own space trip and celebrate World Space Week in your own special way!

This space travel calculator is a comprehensive tool that allows you to estimate many essential parameters in theoretical interstellar space travel . Have you ever wondered how fast we can travel in space, how much time it will take to get to the nearest star or galaxy, or how much fuel it requires? In the following article, using a relativistic rocket equation, we'll try to answer questions like "Is interstellar travel possible?" , and "Can humans travel at the speed of light?"

Explore the world of light-speed travel of (hopefully) future spaceships with our relativistic space travel calculator!

If you're interested in astrophysics, check out our other calculators. Find out the speed required to leave the surface of any planet with the escape velocity calculator or estimate the parameters of the orbital motion of planets using the orbital velocity calculator .

One small step for man, one giant leap for humanity

Although human beings have been dreaming about space travel forever, the first landmark in the history of space travel is Russia's launch of Sputnik 2 into space in November 1957. The spacecraft carried the first earthling, the Russian dog Laika , into space.

Four years later, on 12 April 1961, Soviet cosmonaut Yuri A. Gagarin became the first human in space when his spacecraft, the Vostok 1, completed one orbit of Earth.

The first American astronaut to enter space was Alan Shepard (May 1961). During the Apollo 11 mission in July 1969, Neil Armstrong and Buzz Aldrin became the first men to land on the moon. Between 1969 and 1972, a total of 12 astronauts walked the moon, marking one of the most outstanding achievements for NASA.

In recent decades, space travel technology has seen some incredible advancements. Especially with the advent of private space companies like SpaceX, Virgin Galactic, and Blue Origin, the dream of space tourism is looking more and more realistic for everyone!

However, when it comes to including women, we are yet to make great strides. So far, 566 people have traveled to space. Only 65 of them were women .

Although the first woman in space, a Soviet astronaut Valentina Tereshkova , who orbited Earth 48 times, went into orbit in June 1963. It was only in October 2019 that the first all-female spacewalk was completed by NASA astronauts Jessica Meir and Christina Koch.

Women's access to space is still far from equal, but there are signs of progress, like NASA planning to land the first woman and first person of color on the moon by 2024 with its Artemis missions. World Space Week is also celebrating the achievements and contributions of women in space this year!

In the following sections, we will explore the feasibility of space travel and its associated challenges.

How fast can we travel in space? Is interstellar travel possible?

Interstellar space is a rather empty place. Its temperature is not much more than the coldest possible temperature, i.e., an absolute zero. It equals about 3 kelvins – minus 270 °C or minus 455 °F. You can't find air there, and therefore there is no drag or friction. On the one hand, humans can't survive in such a hostile place without expensive equipment like a spacesuit or a spaceship, but on the other hand, we can make use of space conditions and its emptiness.

The main advantage of future spaceships is that, since they are moving through a vacuum, they can theoretically accelerate to infinite speeds! However, this is only possible in the classical world of relatively low speeds, where Newtonian physics can be applied. Even if it's true, let's imagine, just for a moment, that we live in a world where any speed is allowed. How long will it take to visit the Andromeda Galaxy, the nearest galaxy to the Milky Way?

We will begin our intergalactic travel with a constant acceleration of 1 g (9.81 m/s² or 32.17 ft/s²) because it ensures that the crew experiences the same comfortable gravitational field as the one on Earth. By using this space travel calculator in Newton's universe mode, you can find out that you need about 2200 years to arrive at the nearest galaxy! And, if you want to stop there, you need an additional 1000 years . Nobody lives for 3000 years! Is intergalactic travel impossible for us, then? Luckily, we have good news. We live in a world of relativistic effects, where unusual phenomena readily occur.

Can humans travel at the speed of light? – relativistic space travel

In the previous example, where we traveled to Andromeda Galaxy, the maximum velocity was almost 3000 times greater than the speed of light c = 299,792,458 m/s , or about c = 3 × 10 8 m/s using scientific notation.

However, as velocity increases, relativistic effects start to play an essential role. According to special relativity proposed by Albert Einstein, nothing can exceed the speed of light. How can it help us with interstellar space travel? Doesn't it mean we will travel at a much lower speed? Yes, it does, but there are also a few new relativistic phenomena, including time dilation and length contraction, to name a few. The former is crucial in relativistic space travel.

Time dilation is a difference of time measured by two observers, one being in motion and the second at rest (relative to each other). It is something we are not used to on Earth. Clocks in a moving spaceship tick slower than the same clocks on Earth ! Time passing in a moving spaceship T T T and equivalent time observed on Earth t t t are related by the following formula:

where γ \gamma γ is the Lorentz factor that comprises the speed of the spaceship v v v and the speed of light c c c :

where β = v / c \beta = v/c β = v / c .

For example, if γ = 10 \gamma = 10 γ = 10 ( v = 0.995 c v = 0.995c v = 0.995 c ), then every second passing on Earth corresponds to ten seconds passing in the spaceship. Inside the spacecraft, events take place 90 percent slower; the difference can be even greater for higher velocities. Note that both observers can be in motion, too. In that case, to calculate the relative relativistic velocity, you can use our velocity addition calculator .

Let's go back to our example again, but this time we're in Einstein's universe of relativistic effects trying to reach Andromeda. The time needed to get there, measured by the crew of the spaceship, equals only 15 years ! Well, this is still a long time, but it is more achievable in a practical sense. If you would like to stop at the destination, you should start decelerating halfway through. In this situation, the time passed in the spaceship will be extended by about 13 additional years .

Unfortunately, this is only a one-way journey. You can, of course, go back to Earth, but nothing will be the same. During your interstellar space travel to the Andromeda Galaxy, about 2,500,000 years have passed on Earth. It would be a completely different planet, and nobody could foresee the fate of our civilization.

A similar problem was considered in the first Planet of the Apes movie, where astronauts crash-landed back on Earth. While these astronauts had only aged by 18 months, 2000 years had passed on Earth (sorry for the spoilers, but the film is over 50 years old at this point, you should have seen it by now). How about you? Would you be able to leave everything you know and love about our galaxy forever and begin a life of space exploration?

Space travel calculator – relativistic rocket equation

Now that you know whether interstellar travel is possible and how fast we can travel in space, it's time for some formulas. In this section, you can find the "classical" and relativistic rocket equations that are included in the relativistic space travel calculator.

There could be four combinations since we want to estimate how long it takes to arrive at the destination point at full speed as well as arrive at the destination point and stop. Every set contains distance, time passing on Earth and in the spaceship (only relativity approach), expected maximum velocity and corresponding kinetic energy (on the additional parameters section), and the required fuel mass (see Intergalactic travel — fuel problem section for more information). The notation is:

• a a a — Spaceship acceleration (by default 1   g 1\rm\, g 1 g ). We assume it is positive a > 0 a > 0 a > 0 (at least until halfway) and constant.
• m m m — Spaceship mass. It is required to calculate kinetic energy (and fuel).
• d d d — Distance to the destination. Note that you can select it from the list or type in any other distance to the desired object.
• T T T — Time that passed in a spaceship, or, in other words, how much the crew has aged.
• t t t — Time that passed in a resting frame of reference, e.g., on Earth.
• v v v — Maximum velocity reached by the spaceship.
• K E \rm KE KE — Maximum kinetic energy reached by the spaceship.

The relativistic space travel calculator is dedicated to very long journeys, interstellar or even intergalactic, in which we can neglect the influence of the gravitational field, e.g., from Earth. We didn't include our closest celestial bodies, like the Moon or Mars, in the destination list because it would be pointless. For them, we need different equations that also take into consideration gravitational force.

Newton's universe — arrive at the destination at full speed

It's the simplest case because here, T T T equals t t t for any speed. To calculate the distance covered at constant acceleration during a certain time, you can use the following classical formula:

Since acceleration is constant, and we assume that the initial velocity equals zero, you can estimate the maximum velocity using this equation:

and the corresponding kinetic energy:

Newton's universe — arrive at the destination and stop

In this situation, we accelerate to the halfway point, reach maximum velocity, and then decelerate to stop at the destination point. Distance covered during the same time is, as you may expect, smaller than before:

Acceleration remains positive until we're halfway there (then it is negative – deceleration), so the maximum velocity is:

and the kinetic energy equation is the same as the previous one.

Einstein's universe — arrive at the destination at full speed

The relativistic rocket equation has to consider the effects of light-speed travel. These are not only speed limitations and time dilation but also how every length becomes shorter for a moving observer, which is a phenomenon of special relativity called length contraction. If l l l is the proper length observed in the rest frame and L L L is the length observed by a crew in a spaceship, then:

What does it mean? If a spaceship moves with the velocity of v = 0.995 c v = 0.995c v = 0.995 c , then γ = 10 \gamma = 10 γ = 10 , and the length observed by a moving object is ten times smaller than the real length. For example, the distance to the Andromeda Galaxy equals about 2,520,000 light years with Earth as the frame of reference. For a spaceship moving with v = 0.995 c v = 0.995c v = 0.995 c , it will be "only" 252,200 light years away. That's a 90 percent decrease or a 164 percent difference!

Now you probably understand why special relativity allows us to intergalactic travel. Below you can find the relativistic rocket equation for the case in which you want to arrive at the destination point at full speed (without stopping). You can find its derivation in the book by Messrs Misner, Thorne ( Co-Winner of the 2017 Nobel Prize in Physics ) and Wheller titled Gravitation , section §6.2. Hyperbolic motion. More accessible formulas are in the mathematical physicist John Baez's article The Relativistic Rocket :

• Time passed on Earth:
• Time passed in the spaceship:
• Maximum velocity:
• Relativistic kinetic energy remains the same:

The symbols sh ⁡ \sh sh , ch ⁡ \ch ch , and th ⁡ \th th are, respectively, sine, cosine, and tangent hyperbolic functions, which are analogs of the ordinary trigonometric functions. In turn, sh ⁡ − 1 \sh^{-1} sh − 1 and ch ⁡ − 1 \ch^{-1} ch − 1 are the inverse hyperbolic functions that can be expressed with natural logarithms and square roots, according to the article Inverse hyperbolic functions on Wikipedia.

Einstein's universe – arrive at destination point and stop

Most websites with relativistic rocket equations consider only arriving at the desired place at full speed. If you want to stop there, you should start decelerating at the halfway point. Below, you can find a set of equations estimating interstellar space travel parameters in the situation when you want to stop at the destination point :

Intergalactic travel – fuel problem

So, after all of these considerations, can humans travel at the speed of light, or at least at a speed close to it? Jet-rocket engines need a lot of fuel per unit of weight of the rocket. You can use our rocket equation calculator to see how much fuel you need to obtain a certain velocity (e.g., with an effective exhaust velocity of 4500 m/s).

Hopefully, future spaceships will be able to produce energy from matter-antimatter annihilation. This process releases energy from two particles that have mass (e.g., electron and positron) into photons. These photons may then be shot out at the back of the spaceship and accelerate the spaceship due to the conservation of momentum. If you want to know how much energy is contained in matter, check out our E = mc² calculator , which is about the famous Albert Einstein equation.

Now that you know the maximum amount of energy you can acquire from matter, it's time to estimate how much of it you need for intergalactic travel. Appropriate formulas are derived from the conservation of momentum and energy principles. For the relativistic case:

where e x e^x e x is an exponential function, and for classical case:

Remember that it assumes 100% efficiency! One of the promising future spaceships' power sources is the fusion of hydrogen into helium, which provides energy of 0.008 mc² . As you can see, in this reaction, efficiency equals only 0.8%.

Let's check whether the fuel mass amount is reasonable for sending a mass of 1 kg to the nearest galaxy. With a space travel calculator, you can find out that, even with 100% efficiency, you would need 5,200 tons of fuel to send only 1 kilogram of your spaceship . That's a lot!

So can humans travel at the speed of light? Right now, it seems impossible, but technology is still developing. For example, a photonic laser thruster is a good candidate since it doesn't require any matter to work, only photons. Infinity and beyond is actually within our reach!

How do I calculate the travel time to other planets?

To calculate the time it takes to travel to a specific star or galaxy using the space travel calculator, follow these steps:

• Choose the acceleration : the default mode is 1 g (gravitational field similar to Earth's).
• Enter the spaceship mass , excluding fuel.
• Select the destination : pick the star, planet, or galaxy you want to travel to from the dropdown menu.
• The distance between the Earth and your chosen stars will automatically appear. You can also input the distance in light-years directly if you select the Custom distance option in the previous dropdown.
• Define the aim : select whether you aim to " Arrive at destination and stop " or “ Arrive at destination at full speed ”.
• Pick the calculation mode : opt for either " Einstein's universe " mode for relativistic effects or " Newton's universe " for simpler calculations.
• Time passed in spaceship : estimated time experienced by the crew during the journey. (" Einstein's universe " mode)
• Time passed on Earth : estimated time elapsed on Earth during the trip. (" Einstein's universe " mode)
• Time passed : depends on the frame of reference, e.g., on Earth. (" Newton's universe " mode)
• Required fuel mass : estimated fuel quantity needed for the journey.
• Maximum velocity : maximum speed achieved by the spaceship.

How long does it take to get to space?

It takes about 8.5 minutes for a space shuttle or spacecraft to reach Earth's orbit, i.e., the limit of space where the Earth's atmosphere ends. This dividing line between the Earth's atmosphere and space is called the Kármán line . It happens so quickly because the shuttle goes from zero to around 17,500 miles per hour in those 8.5 minutes .

How fast does the space station travel?

The International Space Station travels at an average speed of 28,000 km/h or 17,500 mph . In a single day, the ISS can make several complete revolutions as it circumnavigates the globe in just 90 minutes . Placed in orbit at an altitude of 350 km , the station is visible to the naked eye, looking like a dot crossing the sky due to its very bright solar panels.

How do I reach the speed of light?

To reach the speed of light, you would have to overcome several obstacles, including:

Mass limit : traveling at the speed of light would mean traveling at 299,792,458 meters per second. But, thanks to Einstein's theory of relativity, we know that an object with non-zero mass cannot reach this speed.

Energy : accelerating to the speed of light would require infinite energy.

Effects of relativity : from the outside, time would slow down, and you would shrink.

Why can't sound travel in space?

Sound can’t travel in space because it is a mechanical wave that requires a medium to propagate — this medium can be solid, liquid, or gas. In space, there is no matter, or at least not enough for sound to propagate. The density of matter in space is of the order 1 particle per cubic centimeter . While on Earth , it's much denser at around 10 20 particles per cubic centimeter .

Dreaming of traveling into space? 🌌 Plan your interstellar travel (even to a Star Trek destination) using this calculator 👨‍🚀! Estimate how fast you can reach your destination and how much fuel you would need 🚀

.css-slt4t3.css-slt4t3{color:#2B3148;background-color:transparent;font-family:"Roboto","Helvetica","Arial",sans-serif;font-size:20px;line-height:24px;overflow:visible;padding-top:0px;position:relative;}.css-slt4t3.css-slt4t3:after{content:'';-webkit-transform:scale(0);-moz-transform:scale(0);-ms-transform:scale(0);transform:scale(0);position:absolute;border:2px solid #EA9430;border-radius:2px;inset:-8px;z-index:1;}.css-slt4t3 .js-external-link-button.link-like,.css-slt4t3 .js-external-link-anchor{color:inherit;border-radius:1px;-webkit-text-decoration:underline;text-decoration:underline;}.css-slt4t3 .js-external-link-button.link-like:hover,.css-slt4t3 .js-external-link-anchor:hover,.css-slt4t3 .js-external-link-button.link-like:active,.css-slt4t3 .js-external-link-anchor:active{text-decoration-thickness:2px;text-shadow:1px 0 0;}.css-slt4t3 .js-external-link-button.link-like:focus-visible,.css-slt4t3 .js-external-link-anchor:focus-visible{outline:transparent 2px dotted;box-shadow:0 0 0 2px #6314E6;}.css-slt4t3 p,.css-slt4t3 div{margin:0px;display:block;}.css-slt4t3 pre{margin:0px;display:block;}.css-slt4t3 pre code{display:block;width:-webkit-fit-content;width:-moz-fit-content;width:fit-content;}.css-slt4t3 pre:not(:first-child){padding-top:8px;}.css-slt4t3 ul,.css-slt4t3 ol{display:block margin:0px;padding-left:20px;}.css-slt4t3 ul li,.css-slt4t3 ol li{padding-top:8px;}.css-slt4t3 ul ul,.css-slt4t3 ol ul,.css-slt4t3 ul ol,.css-slt4t3 ol ol{padding-top:0px;}.css-slt4t3 ul:not(:first-child),.css-slt4t3 ol:not(:first-child){padding-top:4px;} .css-4okk7a{margin:auto;background-color:white;overflow:auto;overflow-wrap:break-word;word-break:break-word;}.css-4okk7a code,.css-4okk7a kbd,.css-4okk7a pre,.css-4okk7a samp{font-family:monospace;}.css-4okk7a code{padding:2px 4px;color:#444;background:#ddd;border-radius:4px;}.css-4okk7a figcaption,.css-4okk7a caption{text-align:center;}.css-4okk7a figcaption{font-size:12px;font-style:italic;overflow:hidden;}.css-4okk7a h3{font-size:1.75rem;}.css-4okk7a h4{font-size:1.5rem;}.css-4okk7a .mathBlock{font-size:24px;-webkit-padding-start:4px;padding-inline-start:4px;}.css-4okk7a .mathBlock .katex{font-size:24px;text-align:left;}.css-4okk7a .math-inline{background-color:#f0f0f0;display:inline-block;font-size:inherit;padding:0 3px;}.css-4okk7a .videoBlock,.css-4okk7a .imageBlock{margin-bottom:16px;}.css-4okk7a .imageBlock__image-align--left,.css-4okk7a .videoBlock__video-align--left{float:left;}.css-4okk7a .imageBlock__image-align--right,.css-4okk7a .videoBlock__video-align--right{float:right;}.css-4okk7a .imageBlock__image-align--center,.css-4okk7a .videoBlock__video-align--center{display:block;margin-left:auto;margin-right:auto;clear:both;}.css-4okk7a .imageBlock__image-align--none,.css-4okk7a .videoBlock__video-align--none{clear:both;margin-left:0;margin-right:0;}.css-4okk7a .videoBlock__video--wrapper{position:relative;padding-bottom:56.25%;height:0;}.css-4okk7a .videoBlock__video--wrapper iframe{position:absolute;top:0;left:0;width:100%;height:100%;}.css-4okk7a .videoBlock__caption{text-align:left;}@font-face{font-family:'KaTeX_AMS';src:url(/katex-fonts/KaTeX_AMS-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_AMS-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_AMS-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Caligraphic';src:url(/katex-fonts/KaTeX_Caligraphic-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Caligraphic-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Caligraphic-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Caligraphic';src:url(/katex-fonts/KaTeX_Caligraphic-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Caligraphic-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Caligraphic-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Fraktur';src:url(/katex-fonts/KaTeX_Fraktur-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Fraktur-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Fraktur-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Fraktur';src:url(/katex-fonts/KaTeX_Fraktur-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Fraktur-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Fraktur-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-BoldItalic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-BoldItalic.woff) format('woff'),url(/katex-fonts/KaTeX_Main-BoldItalic.ttf) format('truetype');font-weight:bold;font-style:italic;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Math';src:url(/katex-fonts/KaTeX_Math-BoldItalic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Math-BoldItalic.woff) format('woff'),url(/katex-fonts/KaTeX_Math-BoldItalic.ttf) format('truetype');font-weight:bold;font-style:italic;}@font-face{font-family:'KaTeX_Math';src:url(/katex-fonts/KaTeX_Math-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Math-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_Math-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Script';src:url(/katex-fonts/KaTeX_Script-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Script-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Script-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size1';src:url(/katex-fonts/KaTeX_Size1-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size1-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size1-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size2';src:url(/katex-fonts/KaTeX_Size2-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size2-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size2-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size3';src:url(/katex-fonts/KaTeX_Size3-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size3-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size3-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size4';src:url(/katex-fonts/KaTeX_Size4-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size4-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size4-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Typewriter';src:url(/katex-fonts/KaTeX_Typewriter-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Typewriter-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Typewriter-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}.css-4okk7a .katex{font:normal 1.21em KaTeX_Main,Times New Roman,serif;line-height:1.2;text-indent:0;text-rendering:auto;}.css-4okk7a .katex *{-ms-high-contrast-adjust:none!important;border-color:currentColor;}.css-4okk7a .katex .katex-version::after{content:'0.13.13';}.css-4okk7a .katex .katex-mathml{position:absolute;clip:rect(1px, 1px, 1px, 1px);padding:0;border:0;height:1px;width:1px;overflow:hidden;}.css-4okk7a .katex .katex-html>.newline{display:block;}.css-4okk7a .katex .base{position:relative;display:inline-block;white-space:nowrap;width:-webkit-min-content;width:-moz-min-content;width:-webkit-min-content;width:-moz-min-content;width:min-content;}.css-4okk7a .katex .strut{display:inline-block;}.css-4okk7a .katex .textbf{font-weight:bold;}.css-4okk7a .katex .textit{font-style:italic;}.css-4okk7a .katex .textrm{font-family:KaTeX_Main;}.css-4okk7a .katex .textsf{font-family:KaTeX_SansSerif;}.css-4okk7a .katex .texttt{font-family:KaTeX_Typewriter;}.css-4okk7a .katex .mathnormal{font-family:KaTeX_Math;font-style:italic;}.css-4okk7a .katex .mathit{font-family:KaTeX_Main;font-style:italic;}.css-4okk7a .katex .mathrm{font-style:normal;}.css-4okk7a .katex .mathbf{font-family:KaTeX_Main;font-weight:bold;}.css-4okk7a .katex .boldsymbol{font-family:KaTeX_Math;font-weight:bold;font-style:italic;}.css-4okk7a .katex .amsrm{font-family:KaTeX_AMS;}.css-4okk7a .katex .mathbb,.css-4okk7a .katex .textbb{font-family:KaTeX_AMS;}.css-4okk7a .katex .mathcal{font-family:KaTeX_Caligraphic;}.css-4okk7a .katex .mathfrak,.css-4okk7a .katex .textfrak{font-family:KaTeX_Fraktur;}.css-4okk7a .katex .mathtt{font-family:KaTeX_Typewriter;}.css-4okk7a .katex .mathscr,.css-4okk7a .katex .textscr{font-family:KaTeX_Script;}.css-4okk7a .katex .mathsf,.css-4okk7a .katex .textsf{font-family:KaTeX_SansSerif;}.css-4okk7a .katex .mathboldsf,.css-4okk7a .katex .textboldsf{font-family:KaTeX_SansSerif;font-weight:bold;}.css-4okk7a .katex .mathitsf,.css-4okk7a .katex .textitsf{font-family:KaTeX_SansSerif;font-style:italic;}.css-4okk7a .katex .mainrm{font-family:KaTeX_Main;font-style:normal;}.css-4okk7a .katex .vlist-t{display:inline-table;table-layout:fixed;border-collapse:collapse;}.css-4okk7a .katex .vlist-r{display:table-row;}.css-4okk7a .katex .vlist{display:table-cell;vertical-align:bottom;position:relative;}.css-4okk7a .katex .vlist>span{display:block;height:0;position:relative;}.css-4okk7a .katex .vlist>span>span{display:inline-block;}.css-4okk7a .katex .vlist>span>.pstrut{overflow:hidden;width:0;}.css-4okk7a .katex .vlist-t2{margin-right:-2px;}.css-4okk7a .katex .vlist-s{display:table-cell;vertical-align:bottom;font-size:1px;width:2px;min-width:2px;}.css-4okk7a .katex .vbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:column;-ms-flex-direction:column;flex-direction:column;-webkit-align-items:baseline;-webkit-box-align:baseline;-ms-flex-align:baseline;align-items:baseline;}.css-4okk7a .katex .hbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:row;-ms-flex-direction:row;flex-direction:row;width:100%;}.css-4okk7a .katex .thinbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:row;-ms-flex-direction:row;flex-direction:row;width:0;max-width:0;}.css-4okk7a .katex .msupsub{text-align:left;}.css-4okk7a .katex .mfrac>span>span{text-align:center;}.css-4okk7a .katex .mfrac .frac-line{display:inline-block;width:100%;border-bottom-style:solid;}.css-4okk7a .katex .mfrac .frac-line,.css-4okk7a .katex .overline .overline-line,.css-4okk7a .katex .underline .underline-line,.css-4okk7a .katex .hline,.css-4okk7a .katex .hdashline,.css-4okk7a .katex .rule{min-height:1px;}.css-4okk7a .katex .mspace{display:inline-block;}.css-4okk7a .katex .llap,.css-4okk7a .katex .rlap,.css-4okk7a .katex .clap{width:0;position:relative;}.css-4okk7a .katex .llap>.inner,.css-4okk7a .katex .rlap>.inner,.css-4okk7a .katex .clap>.inner{position:absolute;}.css-4okk7a .katex .llap>.fix,.css-4okk7a .katex .rlap>.fix,.css-4okk7a .katex .clap>.fix{display:inline-block;}.css-4okk7a .katex .llap>.inner{right:0;}.css-4okk7a .katex .rlap>.inner,.css-4okk7a .katex .clap>.inner{left:0;}.css-4okk7a .katex .clap>.inner>span{margin-left:-50%;margin-right:50%;}.css-4okk7a .katex .rule{display:inline-block;border:solid 0;position:relative;}.css-4okk7a .katex .overline .overline-line,.css-4okk7a .katex .underline .underline-line,.css-4okk7a .katex .hline{display:inline-block;width:100%;border-bottom-style:solid;}.css-4okk7a .katex .hdashline{display:inline-block;width:100%;border-bottom-style:dashed;}.css-4okk7a .katex .sqrt>.root{margin-left:0.27777778em;margin-right:-0.55555556em;}.css-4okk7a .katex .sizing.reset-size1.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size1{font-size:1em;}.css-4okk7a .katex .sizing.reset-size1.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size2{font-size:1.2em;}.css-4okk7a .katex .sizing.reset-size1.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size3{font-size:1.4em;}.css-4okk7a .katex .sizing.reset-size1.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size4{font-size:1.6em;}.css-4okk7a .katex .sizing.reset-size1.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size5{font-size:1.8em;}.css-4okk7a .katex .sizing.reset-size1.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size6{font-size:2em;}.css-4okk7a .katex .sizing.reset-size1.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size7{font-size:2.4em;}.css-4okk7a .katex .sizing.reset-size1.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size8{font-size:2.88em;}.css-4okk7a .katex .sizing.reset-size1.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size9{font-size:3.456em;}.css-4okk7a .katex .sizing.reset-size1.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size10{font-size:4.148em;}.css-4okk7a .katex .sizing.reset-size1.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size11{font-size:4.976em;}.css-4okk7a .katex .sizing.reset-size2.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size1{font-size:0.83333333em;}.css-4okk7a .katex .sizing.reset-size2.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size2{font-size:1em;}.css-4okk7a .katex .sizing.reset-size2.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size3{font-size:1.16666667em;}.css-4okk7a .katex .sizing.reset-size2.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size4{font-size:1.33333333em;}.css-4okk7a .katex .sizing.reset-size2.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size5{font-size:1.5em;}.css-4okk7a .katex .sizing.reset-size2.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size6{font-size:1.66666667em;}.css-4okk7a .katex .sizing.reset-size2.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size7{font-size:2em;}.css-4okk7a .katex .sizing.reset-size2.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size8{font-size:2.4em;}.css-4okk7a .katex .sizing.reset-size2.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size9{font-size:2.88em;}.css-4okk7a .katex .sizing.reset-size2.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size10{font-size:3.45666667em;}.css-4okk7a .katex .sizing.reset-size2.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size11{font-size:4.14666667em;}.css-4okk7a .katex .sizing.reset-size3.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size1{font-size:0.71428571em;}.css-4okk7a .katex .sizing.reset-size3.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size2{font-size:0.85714286em;}.css-4okk7a .katex .sizing.reset-size3.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size3{font-size:1em;}.css-4okk7a .katex .sizing.reset-size3.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size4{font-size:1.14285714em;}.css-4okk7a .katex .sizing.reset-size3.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size5{font-size:1.28571429em;}.css-4okk7a .katex .sizing.reset-size3.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size6{font-size:1.42857143em;}.css-4okk7a .katex .sizing.reset-size3.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size7{font-size:1.71428571em;}.css-4okk7a .katex .sizing.reset-size3.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size8{font-size:2.05714286em;}.css-4okk7a .katex .sizing.reset-size3.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size9{font-size:2.46857143em;}.css-4okk7a .katex .sizing.reset-size3.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size10{font-size:2.96285714em;}.css-4okk7a .katex .sizing.reset-size3.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size11{font-size:3.55428571em;}.css-4okk7a .katex .sizing.reset-size4.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size1{font-size:0.625em;}.css-4okk7a .katex .sizing.reset-size4.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size2{font-size:0.75em;}.css-4okk7a .katex .sizing.reset-size4.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size3{font-size:0.875em;}.css-4okk7a .katex .sizing.reset-size4.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size4{font-size:1em;}.css-4okk7a .katex .sizing.reset-size4.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size5{font-size:1.125em;}.css-4okk7a .katex .sizing.reset-size4.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size6{font-size:1.25em;}.css-4okk7a .katex .sizing.reset-size4.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size7{font-size:1.5em;}.css-4okk7a .katex .sizing.reset-size4.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size8{font-size:1.8em;}.css-4okk7a .katex .sizing.reset-size4.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size9{font-size:2.16em;}.css-4okk7a .katex .sizing.reset-size4.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size10{font-size:2.5925em;}.css-4okk7a .katex .sizing.reset-size4.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size11{font-size:3.11em;}.css-4okk7a .katex .sizing.reset-size5.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size1{font-size:0.55555556em;}.css-4okk7a .katex .sizing.reset-size5.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size2{font-size:0.66666667em;}.css-4okk7a .katex .sizing.reset-size5.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size3{font-size:0.77777778em;}.css-4okk7a .katex .sizing.reset-size5.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size4{font-size:0.88888889em;}.css-4okk7a .katex .sizing.reset-size5.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size5{font-size:1em;}.css-4okk7a .katex .sizing.reset-size5.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size6{font-size:1.11111111em;}.css-4okk7a .katex .sizing.reset-size5.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size7{font-size:1.33333333em;}.css-4okk7a .katex .sizing.reset-size5.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size8{font-size:1.6em;}.css-4okk7a .katex .sizing.reset-size5.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size9{font-size:1.92em;}.css-4okk7a .katex .sizing.reset-size5.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size10{font-size:2.30444444em;}.css-4okk7a .katex .sizing.reset-size5.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size11{font-size:2.76444444em;}.css-4okk7a .katex .sizing.reset-size6.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size1{font-size:0.5em;}.css-4okk7a .katex .sizing.reset-size6.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size2{font-size:0.6em;}.css-4okk7a .katex .sizing.reset-size6.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size3{font-size:0.7em;}.css-4okk7a .katex .sizing.reset-size6.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size4{font-size:0.8em;}.css-4okk7a .katex .sizing.reset-size6.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size5{font-size:0.9em;}.css-4okk7a .katex .sizing.reset-size6.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size6{font-size:1em;}.css-4okk7a .katex .sizing.reset-size6.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size7{font-size:1.2em;}.css-4okk7a .katex .sizing.reset-size6.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size8{font-size:1.44em;}.css-4okk7a .katex .sizing.reset-size6.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size9{font-size:1.728em;}.css-4okk7a .katex .sizing.reset-size6.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size10{font-size:2.074em;}.css-4okk7a .katex .sizing.reset-size6.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size11{font-size:2.488em;}.css-4okk7a .katex .sizing.reset-size7.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size1{font-size:0.41666667em;}.css-4okk7a .katex .sizing.reset-size7.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size2{font-size:0.5em;}.css-4okk7a .katex .sizing.reset-size7.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size3{font-size:0.58333333em;}.css-4okk7a .katex .sizing.reset-size7.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size4{font-size:0.66666667em;}.css-4okk7a .katex .sizing.reset-size7.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size5{font-size:0.75em;}.css-4okk7a .katex .sizing.reset-size7.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size6{font-size:0.83333333em;}.css-4okk7a .katex .sizing.reset-size7.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size7{font-size:1em;}.css-4okk7a .katex .sizing.reset-size7.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size8{font-size:1.2em;}.css-4okk7a .katex .sizing.reset-size7.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size9{font-size:1.44em;}.css-4okk7a .katex .sizing.reset-size7.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size10{font-size:1.72833333em;}.css-4okk7a .katex .sizing.reset-size7.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size11{font-size:2.07333333em;}.css-4okk7a .katex .sizing.reset-size8.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size1{font-size:0.34722222em;}.css-4okk7a .katex .sizing.reset-size8.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size2{font-size:0.41666667em;}.css-4okk7a .katex .sizing.reset-size8.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size3{font-size:0.48611111em;}.css-4okk7a .katex .sizing.reset-size8.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size4{font-size:0.55555556em;}.css-4okk7a .katex .sizing.reset-size8.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size5{font-size:0.625em;}.css-4okk7a .katex .sizing.reset-size8.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size6{font-size:0.69444444em;}.css-4okk7a .katex .sizing.reset-size8.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size7{font-size:0.83333333em;}.css-4okk7a .katex .sizing.reset-size8.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size8{font-size:1em;}.css-4okk7a .katex .sizing.reset-size8.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size9{font-size:1.2em;}.css-4okk7a .katex .sizing.reset-size8.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size10{font-size:1.44027778em;}.css-4okk7a .katex .sizing.reset-size8.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size11{font-size:1.72777778em;}.css-4okk7a .katex .sizing.reset-size9.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size1{font-size:0.28935185em;}.css-4okk7a .katex .sizing.reset-size9.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size2{font-size:0.34722222em;}.css-4okk7a .katex .sizing.reset-size9.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size3{font-size:0.40509259em;}.css-4okk7a .katex .sizing.reset-size9.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size4{font-size:0.46296296em;}.css-4okk7a .katex .sizing.reset-size9.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size5{font-size:0.52083333em;}.css-4okk7a .katex .sizing.reset-size9.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size6{font-size:0.5787037em;}.css-4okk7a .katex .sizing.reset-size9.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size7{font-size:0.69444444em;}.css-4okk7a .katex .sizing.reset-size9.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size8{font-size:0.83333333em;}.css-4okk7a .katex .sizing.reset-size9.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size9{font-size:1em;}.css-4okk7a .katex .sizing.reset-size9.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size10{font-size:1.20023148em;}.css-4okk7a .katex .sizing.reset-size9.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size11{font-size:1.43981481em;}.css-4okk7a .katex .sizing.reset-size10.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size1{font-size:0.24108004em;}.css-4okk7a .katex .sizing.reset-size10.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size2{font-size:0.28929605em;}.css-4okk7a .katex .sizing.reset-size10.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size3{font-size:0.33751205em;}.css-4okk7a .katex .sizing.reset-size10.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size4{font-size:0.38572806em;}.css-4okk7a .katex .sizing.reset-size10.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size5{font-size:0.43394407em;}.css-4okk7a .katex .sizing.reset-size10.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size6{font-size:0.48216008em;}.css-4okk7a .katex .sizing.reset-size10.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size7{font-size:0.57859209em;}.css-4okk7a .katex .sizing.reset-size10.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size8{font-size:0.69431051em;}.css-4okk7a .katex .sizing.reset-size10.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size9{font-size:0.83317261em;}.css-4okk7a .katex .sizing.reset-size10.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size10{font-size:1em;}.css-4okk7a .katex .sizing.reset-size10.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size11{font-size:1.19961427em;}.css-4okk7a .katex .sizing.reset-size11.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size1{font-size:0.20096463em;}.css-4okk7a .katex .sizing.reset-size11.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size2{font-size:0.24115756em;}.css-4okk7a .katex .sizing.reset-size11.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size3{font-size:0.28135048em;}.css-4okk7a .katex .sizing.reset-size11.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size4{font-size:0.32154341em;}.css-4okk7a .katex .sizing.reset-size11.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size5{font-size:0.36173633em;}.css-4okk7a .katex .sizing.reset-size11.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size6{font-size:0.40192926em;}.css-4okk7a .katex .sizing.reset-size11.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size7{font-size:0.48231511em;}.css-4okk7a .katex .sizing.reset-size11.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size8{font-size:0.57877814em;}.css-4okk7a .katex .sizing.reset-size11.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size9{font-size:0.69453376em;}.css-4okk7a .katex .sizing.reset-size11.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size10{font-size:0.83360129em;}.css-4okk7a .katex .sizing.reset-size11.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size11{font-size:1em;}.css-4okk7a .katex .delimsizing.size1{font-family:KaTeX_Size1;}.css-4okk7a .katex .delimsizing.size2{font-family:KaTeX_Size2;}.css-4okk7a .katex .delimsizing.size3{font-family:KaTeX_Size3;}.css-4okk7a .katex .delimsizing.size4{font-family:KaTeX_Size4;}.css-4okk7a .katex .delimsizing.mult .delim-size1>span{font-family:KaTeX_Size1;}.css-4okk7a .katex .delimsizing.mult .delim-size4>span{font-family:KaTeX_Size4;}.css-4okk7a .katex .nulldelimiter{display:inline-block;width:0.12em;}.css-4okk7a .katex .delimcenter{position:relative;}.css-4okk7a .katex .op-symbol{position:relative;}.css-4okk7a .katex .op-symbol.small-op{font-family:KaTeX_Size1;}.css-4okk7a .katex .op-symbol.large-op{font-family:KaTeX_Size2;}.css-4okk7a .katex .op-limits>.vlist-t{text-align:center;}.css-4okk7a .katex .accent>.vlist-t{text-align:center;}.css-4okk7a .katex .accent .accent-body{position:relative;}.css-4okk7a .katex .accent .accent-body:not(.accent-full){width:0;}.css-4okk7a .katex .overlay{display:block;}.css-4okk7a .katex .mtable .vertical-separator{display:inline-block;min-width:1px;}.css-4okk7a .katex .mtable .arraycolsep{display:inline-block;}.css-4okk7a .katex .mtable .col-align-c>.vlist-t{text-align:center;}.css-4okk7a .katex .mtable .col-align-l>.vlist-t{text-align:left;}.css-4okk7a .katex .mtable .col-align-r>.vlist-t{text-align:right;}.css-4okk7a .katex .svg-align{text-align:left;}.css-4okk7a .katex svg{display:block;position:absolute;width:100%;height:inherit;fill:currentColor;stroke:currentColor;fill-rule:nonzero;fill-opacity:1;stroke-width:1;stroke-linecap:butt;stroke-linejoin:miter;stroke-miterlimit:4;stroke-dasharray:none;stroke-dashoffset:0;stroke-opacity:1;}.css-4okk7a .katex svg path{stroke:none;}.css-4okk7a .katex img{border-style:none;min-width:0;min-height:0;max-width:none;max-height:none;}.css-4okk7a .katex .stretchy{width:100%;display:block;position:relative;overflow:hidden;}.css-4okk7a .katex .stretchy::before,.css-4okk7a .katex .stretchy::after{content:'';}.css-4okk7a .katex .hide-tail{width:100%;position:relative;overflow:hidden;}.css-4okk7a .katex .halfarrow-left{position:absolute;left:0;width:50.2%;overflow:hidden;}.css-4okk7a .katex .halfarrow-right{position:absolute;right:0;width:50.2%;overflow:hidden;}.css-4okk7a .katex .brace-left{position:absolute;left:0;width:25.1%;overflow:hidden;}.css-4okk7a .katex .brace-center{position:absolute;left:25%;width:50%;overflow:hidden;}.css-4okk7a .katex .brace-right{position:absolute;right:0;width:25.1%;overflow:hidden;}.css-4okk7a .katex .x-arrow-pad{padding:0 0.5em;}.css-4okk7a .katex .cd-arrow-pad{padding:0 0.55556em 0 0.27778em;}.css-4okk7a .katex .x-arrow,.css-4okk7a .katex .mover,.css-4okk7a .katex .munder{text-align:center;}.css-4okk7a .katex .boxpad{padding:0 0.3em 0 0.3em;}.css-4okk7a .katex .fbox,.css-4okk7a .katex .fcolorbox{box-sizing:border-box;border:0.04em solid;}.css-4okk7a .katex .cancel-pad{padding:0 0.2em 0 0.2em;}.css-4okk7a .katex .cancel-lap{margin-left:-0.2em;margin-right:-0.2em;}.css-4okk7a .katex .sout{border-bottom-style:solid;border-bottom-width:0.08em;}.css-4okk7a .katex .angl{box-sizing:border-box;border-top:0.049em solid;border-right:0.049em solid;margin-right:0.03889em;}.css-4okk7a .katex .anglpad{padding:0 0.03889em 0 0.03889em;}.css-4okk7a .katex .eqn-num::before{counter-increment:katexEqnNo;content:'(' counter(katexEqnNo) ')';}.css-4okk7a .katex .mml-eqn-num::before{counter-increment:mmlEqnNo;content:'(' counter(mmlEqnNo) ')';}.css-4okk7a .katex .mtr-glue{width:50%;}.css-4okk7a .katex .cd-vert-arrow{display:inline-block;position:relative;}.css-4okk7a .katex .cd-label-left{display:inline-block;position:absolute;right:calc(50% + 0.3em);text-align:left;}.css-4okk7a .katex .cd-label-right{display:inline-block;position:absolute;left:calc(50% + 0.3em);text-align:right;}.css-4okk7a .katex-display{display:block;margin:1em 0;text-align:center;}.css-4okk7a .katex-display>.katex{display:block;white-space:nowrap;}.css-4okk7a .katex-display>.katex>.katex-html{display:block;position:relative;}.css-4okk7a .katex-display>.katex>.katex-html>.tag{position:absolute;right:0;}.css-4okk7a .katex-display.leqno>.katex>.katex-html>.tag{left:0;right:auto;}.css-4okk7a .katex-display.fleqn>.katex{text-align:left;padding-left:2em;}.css-4okk7a body{counter-reset:katexEqnNo mmlEqnNo;}.css-4okk7a table{width:-webkit-max-content;width:-moz-max-content;width:max-content;}.css-4okk7a .tableBlock{max-width:100%;margin-bottom:1rem;overflow-y:scroll;}.css-4okk7a .tableBlock thead,.css-4okk7a .tableBlock thead th{border-bottom:1px solid #333!important;}.css-4okk7a .tableBlock th,.css-4okk7a .tableBlock td{padding:10px;text-align:left;}.css-4okk7a .tableBlock th{font-weight:bold!important;}.css-4okk7a .tableBlock caption{caption-side:bottom;color:#555;font-size:12px;font-style:italic;text-align:center;}.css-4okk7a .tableBlock caption>p{margin:0;}.css-4okk7a .tableBlock th>p,.css-4okk7a .tableBlock td>p{margin:0;}.css-4okk7a .tableBlock [data-background-color='aliceblue']{background-color:#f0f8ff;color:#000;}.css-4okk7a .tableBlock [data-background-color='black']{background-color:#000;color:#fff;}.css-4okk7a .tableBlock [data-background-color='chocolate']{background-color:#d2691e;color:#fff;}.css-4okk7a .tableBlock [data-background-color='cornflowerblue']{background-color:#6495ed;color:#fff;}.css-4okk7a .tableBlock [data-background-color='crimson']{background-color:#dc143c;color:#fff;}.css-4okk7a .tableBlock [data-background-color='darkblue']{background-color:#00008b;color:#fff;}.css-4okk7a .tableBlock [data-background-color='darkseagreen']{background-color:#8fbc8f;color:#000;}.css-4okk7a .tableBlock [data-background-color='deepskyblue']{background-color:#00bfff;color:#000;}.css-4okk7a .tableBlock [data-background-color='gainsboro']{background-color:#dcdcdc;color:#000;}.css-4okk7a .tableBlock [data-background-color='grey']{background-color:#808080;color:#fff;}.css-4okk7a .tableBlock [data-background-color='lemonchiffon']{background-color:#fffacd;color:#000;}.css-4okk7a .tableBlock [data-background-color='lightpink']{background-color:#ffb6c1;color:#000;}.css-4okk7a .tableBlock [data-background-color='lightsalmon']{background-color:#ffa07a;color:#000;}.css-4okk7a .tableBlock [data-background-color='lightskyblue']{background-color:#87cefa;color:#000;}.css-4okk7a .tableBlock [data-background-color='mediumblue']{background-color:#0000cd;color:#fff;}.css-4okk7a .tableBlock [data-background-color='omnigrey']{background-color:#f0f0f0;color:#000;}.css-4okk7a .tableBlock [data-background-color='white']{background-color:#fff;color:#000;}.css-4okk7a .tableBlock [data-text-align='center']{text-align:center;}.css-4okk7a .tableBlock [data-text-align='left']{text-align:left;}.css-4okk7a .tableBlock [data-text-align='right']{text-align:right;}.css-4okk7a .tableBlock [data-vertical-align='bottom']{vertical-align:bottom;}.css-4okk7a .tableBlock [data-vertical-align='middle']{vertical-align:middle;}.css-4okk7a .tableBlock [data-vertical-align='top']{vertical-align:top;}.css-4okk7a .tableBlock__font-size--xxsmall{font-size:10px;}.css-4okk7a .tableBlock__font-size--xsmall{font-size:12px;}.css-4okk7a .tableBlock__font-size--small{font-size:14px;}.css-4okk7a .tableBlock__font-size--large{font-size:18px;}.css-4okk7a .tableBlock__border--some tbody tr:not(:last-child){border-bottom:1px solid #e2e5e7;}.css-4okk7a .tableBlock__border--bordered td,.css-4okk7a .tableBlock__border--bordered th{border:1px solid #e2e5e7;}.css-4okk7a .tableBlock__border--borderless tbody+tbody,.css-4okk7a .tableBlock__border--borderless td,.css-4okk7a .tableBlock__border--borderless th,.css-4okk7a .tableBlock__border--borderless tr,.css-4okk7a .tableBlock__border--borderless thead,.css-4okk7a .tableBlock__border--borderless thead th{border:0!important;}.css-4okk7a .tableBlock:not(.tableBlock__table-striped) tbody tr{background-color:unset!important;}.css-4okk7a .tableBlock__table-striped tbody tr:nth-of-type(odd){background-color:#f9fafc!important;}.css-4okk7a .tableBlock__table-compactl th,.css-4okk7a .tableBlock__table-compact td{padding:3px!important;}.css-4okk7a .tableBlock__full-size{width:100%;}.css-4okk7a .textBlock{margin-bottom:16px;}.css-4okk7a .textBlock__text-formatting--finePrint{font-size:12px;}.css-4okk7a .textBlock__text-infoBox{padding:0.75rem 1.25rem;margin-bottom:1rem;border:1px solid transparent;border-radius:0.25rem;}.css-4okk7a .textBlock__text-infoBox p{margin:0;}.css-4okk7a .textBlock__text-infoBox--primary{background-color:#cce5ff;border-color:#b8daff;color:#004085;}.css-4okk7a .textBlock__text-infoBox--secondary{background-color:#e2e3e5;border-color:#d6d8db;color:#383d41;}.css-4okk7a .textBlock__text-infoBox--success{background-color:#d4edda;border-color:#c3e6cb;color:#155724;}.css-4okk7a .textBlock__text-infoBox--danger{background-color:#f8d7da;border-color:#f5c6cb;color:#721c24;}.css-4okk7a .textBlock__text-infoBox--warning{background-color:#fff3cd;border-color:#ffeeba;color:#856404;}.css-4okk7a .textBlock__text-infoBox--info{background-color:#d1ecf1;border-color:#bee5eb;color:#0c5460;}.css-4okk7a .textBlock__text-infoBox--dark{background-color:#d6d8d9;border-color:#c6c8ca;color:#1b1e21;}.css-4okk7a .text-overline{-webkit-text-decoration:overline;text-decoration:overline;}.css-4okk7a.css-4okk7a{color:#2B3148;background-color:transparent;font-family:"Roboto","Helvetica","Arial",sans-serif;font-size:20px;line-height:24px;overflow:visible;padding-top:0px;position:relative;}.css-4okk7a.css-4okk7a:after{content:'';-webkit-transform:scale(0);-moz-transform:scale(0);-ms-transform:scale(0);transform:scale(0);position:absolute;border:2px solid #EA9430;border-radius:2px;inset:-8px;z-index:1;}.css-4okk7a .js-external-link-button.link-like,.css-4okk7a .js-external-link-anchor{color:inherit;border-radius:1px;-webkit-text-decoration:underline;text-decoration:underline;}.css-4okk7a .js-external-link-button.link-like:hover,.css-4okk7a .js-external-link-anchor:hover,.css-4okk7a .js-external-link-button.link-like:active,.css-4okk7a .js-external-link-anchor:active{text-decoration-thickness:2px;text-shadow:1px 0 0;}.css-4okk7a .js-external-link-button.link-like:focus-visible,.css-4okk7a .js-external-link-anchor:focus-visible{outline:transparent 2px dotted;box-shadow:0 0 0 2px #6314E6;}.css-4okk7a p,.css-4okk7a div{margin:0px;display:block;}.css-4okk7a pre{margin:0px;display:block;}.css-4okk7a pre code{display:block;width:-webkit-fit-content;width:-moz-fit-content;width:fit-content;}.css-4okk7a pre:not(:first-child){padding-top:8px;}.css-4okk7a ul,.css-4okk7a ol{display:block margin:0px;padding-left:20px;}.css-4okk7a ul li,.css-4okk7a ol li{padding-top:8px;}.css-4okk7a ul ul,.css-4okk7a ol ul,.css-4okk7a ul ol,.css-4okk7a ol ol{padding-top:0px;}.css-4okk7a ul:not(:first-child),.css-4okk7a ol:not(:first-child){padding-top:4px;} Spaceship and destination 👩‍🚀👨‍🚀

Spaceship acceleration

Spaceship mass

Mass of spaceship excluding fuel.

Destination

Select a destination from the list or type in distance by hand.

Which star/galaxy?

If you want to input your own distance, select the 'Custom destination' option in the 'Which star/galaxy?' field.

Calculation options

Do you want to stop at destination point? If yes, the spaceship will start decelerating once it reaches the halfway point.

Calculations mode

You can compare Einstein's special relativity with non-relativistic Newton's physics. Remember that at near-light speeds only the former is correct!

Travel details 🚀

Time passed in spaceship

Time passed on Earth

Time passed in the resting frame of reference. It could be an observer on Earth.

Required fuel mass

Assuming 100% efficiency.

Maximum velocity

Note that our calculator may round velocity to the speed of light if it is really close to it.

Additional parameters

Fuel energy equivalent

Required fuel mass multiplied by c².

Maximum kinetic energy

Beta parameter for the maximum velocity.

γ [1/√(1 - β²)]

Lorentz factor for the maximum velocity.

Escape Velocity Formula

You must have seen rockets leaving the earth to go into space. Then you must have also noticed they require a very huge kick-start in order to leave the surface of the earth. It is because of the strong gravitational field of the surface of the earth. Thus, this is where escape velocity comes in. In this article, you will learn about the escape velocity formula and see how the formula can be used to find out the escape velocity of any object or body.

Escape Velocity is referred to as the minimum velocity needed by anybody or object to be projected to overcome the gravitational pull of the planet earth. In other words, the minimum velocity that one requires to escape the gravitational field is escape velocity.

Basically, it means escaping the land without any chance of falling back. Therefore, any object or body having escape velocity on the surface of the earth can totally escape the gravitational field of the earth in addition to avoiding the losses due to the atmosphere.

For instance, if you see that a spacecraft leaves the earth’s surface it requires a speed of 7 miles per second or about 25,000 miles per hour to leave the earth without ever falling back to the surface of the earth.

You can download Escape Velocity Cheat Sheet by clicking on the download button below

Escape velocity refers to the minimum velocity which is needed to leave a planet or moon. For instance, for any rocket or some other object to leave a planet, it has to overcome the pull of gravity.

The formula for escape velocity comprises of a constant, G, which we refer to as the universal gravitational constant. The value of it is = 6.673 × 10-11 N . m2 / kg2. The unit for escape velocity is meters per second (m/s).

Escape velocity = \(\sqrt{\frac{2 (gravitational constant) (mass of the planet of moon) }{radius of the planet or moon}}\)

v escape = \(\sqrt{\frac{2GM}{R}}\)

Over here: v escape refers to the escape velocity (m/s) G is the universal gravitational constant (6.673 × 10-11 N . m2 / kg2) M refers to the mass of the planet or moon (kg) R is the radius of the planet or moon (m)

 Solved Question

Question – Suppose the radius of Earth is 6.38 × 106 m and the mass of the planet earth is 5.98 × 1024 kg. Find out the escape velocity from planet earth.

Answer – We can find the escape velocity from earth using the escape velocity formula:

vescape = \(\sqrt{\frac{2GM}{R}}\) Thus, when we replace it with figures, we will get: vescape = \(\sqrt{\frac{2(6.673 \times 10^{-11}N^{.}m^{2}/kg^{2})(5.98 \times 10^{24}kg)}{6.38 \times 10^{6}m}}\) \(v_{escape} = \sqrt{\frac{7.981 \times 10^{14}N \cdot m^{2}/kg}{6.38 \times 10^{6}m}}\) vescape = \(\sqrt{1.251\times 10^{8} N \cdot m^{2}/kg}\) vescape = 11184 m/s

Therefore, the escape velocity from Earth is 11 184 m/s, or approximately 11.2 km/s.

Question – In order to leave the moon, the Apollo astronauts had to take off in the lunar mobile and reach the escape velocity of the moon. The radius of the moon is 1.74 × 106 m, and the mass of the moon is 7.35 × 1022 kg. Calculate the velocity which the Apollo astronauts have to reach in order to leave the moon?

Answer – We can find the escape velocity from the moon using the escape velocity formula: vescape = \(\sqrt{\frac{2GM}{R}}\) \(v_{escape} = \sqrt{\frac{2(6.673 \times 10 ^{-11}N \cdot m^{2}/kg^{2}) (7.35 \times 10^{22}kg)}{1.74 \times 10^{6}m}}\) \(v_{escape} = \sqrt{\frac{9.809 \times 10 ^{-11}N \cdot m^{2}/kg}{1.74 \times 10^{6}m}}\) \(v_{escape} = \sqrt{5.638 \times 10^{6}N \cdot m^{2}/kg}\) $$v_{escape} = 2374$$ m/s.

Therefore, the escape velocity from the moon is 2374 m/s, or almost 2.37 km/s.

Customize your course in 30 seconds

Which class are you in.

Physics Formulas

• Parallel Axis Theorem Formula
• Optics Formula
• Universal Gravitation Formula
• Physics Kinematics Formulas
• Photoelectric Effect Formula
• Momentum Of Photon Formula
• DC Voltage Drop Formula
• Energy of a Wave Formula
• Uncertainty Principle Formula
• Spring Potential Energy Formula

5 responses to “Spring Potential Energy Formula”

Typo Error> Speed of Light, C = 299,792,458 m/s in vacuum So U s/b C = 3 x 10^8 m/s Not that C = 3 x 108 m/s to imply C = 324 m/s A bullet is faster than 324m/s

I have realy intrested to to this topic

m=f/a correct this

Interesting studies

It is already correct f= ma by second newton formula…

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Download the App

The Life of Konstantin Tsiolkovsky, Rocket Science Pioneer

Courtesy of the New Mexico Museum of Space History

• An Introduction to Astronomy
• Important Astronomers
• Solar System
• Stars, Planets, and Galaxies
• Space Exploration
• Weather & Climate

• M.S., Journalism and Mass Communications, University of Colorado - Boulder
• B.S., Education, University of Colorado

Konstantin E. Tsiolkovsky (September 17, 1857 – September 19, 1935) was a scientist, mathematician, and theoretician whose work became the basis for the development of rocket science in the Soviet Union. During his lifetime, he speculated about the possibility of sending people into space. Inspired by science fiction writer Jules Verne and his stories of space travel, Tsiolkovsky became known as the "father of rocket science and dynamics" whose work directly led to his country's involvement in the space race.

Early Years

Konstantin Eduardovich Tsiolkovsky was born on September 17, 1857 in Ishevskoye, Russia. His parents were Polish; they raised 17 children in the harsh environment of Siberia. They recognized the young Konstantin's great interest in science, even as he suffered an attack of scarlet fever at the age of 10. This illness took away his hearing, and his formal schooling came to an end for a while, although he continued to learn by reading at home.

Eventually, Tsiolkovsky was able to gain enough education to start college in Moscow. He finished his education and qualified to become a teacher, working in a school in a town called Borovsk. That is where he married Varvara Sokolova. Together, they raised two children, Ignaty and Lyubov. He spent much of his life living in Kaluga, a small village near Moscow.

Developing the Principles of Rocketry

Tsiokovsky began his development of rocketry by considering philosophical principles of flight. Over the course of his career, he ultimately wrote more than 400 papers on that and related subjects. His first works began in the late 1800s when he wrote a paper called "Theory of Gases." In it, he examined the kinetics of gases, and then went on to study the theories of flight, aerodynamics, and the technical requirements for airships and other vehicles.

Tsiokovsky continued exploring a variety of flight issues, and in 1903, he published "The Exploration of Cosmic Space by Means of Reaction Devices." His calculations for achieving orbit, along with designs for rocket craft set the stage for later developments. He focused on specifics of rocket flight, and his rocket equation related the change in velocity for a rocket to the effective exhaust velocity (that is, how fast the rocket goes per unit of fuel it consumes). This came to be known as the "specific impulse." It also takes into account the mass of the rocket at the beginning of launch and its mass when the launch is finished.

He went on to work on solving problems in rocket flight, focusing on the role of rocket fuel in lofting a vehicle to space. He published the second part to his earlier work, where he discussed the effort a rocket must expend to overcome the force of gravity.

Tsiolkovsky stopped working on astronautics prior to World War I and spent the post-war years teaching mathematics. He was honored for his earlier work on astronautics by the newly formed Soviet government, which supplied backing for his continued research. Konstantin Tsiolkovsky died in 1935 and all his papers became the property of the Soviet state. For a while, they remained a closely guarded state secret. Nonetheless, his work influenced a generation of rocket scientists around the world.

Tsiolkovsky's Legacy

In addition to his theoretical work, Konstantin Tsiolkovsky developed aerodynamics test systems and studied the mechanics of flight. His papers covered aspects of dirigible design and flight, as well as the development of powered airplanes with light fuselages. Thanks to his deep research into principles of rocket flight, he has long been considered the father of rocket science and dynamics. Ideas based on his work informed later achievements by such well-known Soviet rocket experts as Sergei Korolev — an aircraft designer who became the chief rocket engineer for the Soviet Union's space efforts. The rocket engineer designer Valentin Glushko was also a follower of his work, and later in the early 20th century, German rocket expert Hermann Oberth was influenced by his research.

Tsiolkovsky is also often cited as the developer of astronautic theory. This body of work deals with the physics of navigation in space. To develop that, he carefully considered the types of masses that could be delivered to space, the conditions they would face in orbit, and how both rockets and astronauts would survive in the conditions of low Earth orbit. Without his painstaking research and writing, it's quite likely that modern aeronautics and astronautics would not have advanced as fast as it did. Along with Hermann Oberth and Robert H. Goddard , Konstantin Tsiolkovsky is considered one of the three fathers of modern rocketry.

Honors and Recognition

Konstantin Tsiolkovsky was honored during his lifetime by the Soviet government, which elected him to the Socialist Academy in 1913. A monument to the Conquerors of Space in Moscow contains a statue of him. A crater on the Moon is named for him, and among other more modern honors, there was a Google Doodle created to honor his legacy. He was also honored on a commemorative coin in 1987.

Konstantin Tsiolkovsky Fast Facts

• Full Name : Konstantin Eduoardovich Tsiolkovsky
• Occupation : Researcher and theorist 
• Born : Sept. 17, 1857 in Izhevskoye, Russian Empire
• Parents : Eduoard Tsiolkovsky, mother: name not known
• Died : September 19, 1935 in Kaluka, Former Soviet Union
• Education : self-educated, became a teacher; attended college in Moscow.
• Key Publications : Investigations of Outer Space by Rocket Devices  (1911), Aims of Astronauts (1914)
• Spouse's Name : Varvara Sokolova
• Children : Ignaty (son); Lyubov (daughter)
• Research Area : Principles of aeronautics and astronautics
• Dunbar, Brian. “Konstantin E. Tsiolkovsky.” NASA, NASA, 5 June 2013, www.nasa.gov/audience/foreducators/rocketry/home/konstantin-tsiolkovsky.html.
• European Space Agency, "Konstantin Tsiolkovsky". ESA, 22 October 2004, http://www.esa.int/Our_Activities/Human_Spaceflight/Exploration/Konstantin_Tsiolkovsky
• Petersen, C.C. Space Exploration: Past, Present, Future. Amberley Books, England, 2017. 
• The Life and Legacy of Hermann Oberth, German Rocket Theorist
• The History of Early Fireworks and Fire Arrows
• Invention and History of Rockets
• Model Rockets: A Great Way to Learn about Spaceflight
• A Historical Timeline of Rockets
• Biography of Kazimir Malevich, Russian Abstract Art Pioneer
• Biography of Robert H. Goddard, American Rocket Scientist
• Rocket Stability and Flight Control Systems
• The Story of Sputnik 1
• Alan Shepard: First American in Space
• A Short History of Roscosmos and the Soviet Space Program
• Redstone Rockets Are a Piece of Space Exploration History
• Valentina Tereshkova: The First Woman in Space
• Biography of Yuri Gagarin, First Man in Space
• Space Chimps and their Flight Histories
• Laika, the First Animal in Outer Space

Konstantin Tsiolkovsky: Russian Father of Rocketry

Konstantin Tsiolkovsky, the Russian father of rocketry, was a self-educated man, but he developed insights into space travel and rocket science that are still in use over a hundred years later, earning him a place in history as one of the pioneers of astronautics.

Konstantin Eduardovich Tsiolkovsky was the fifth of 18 children born to an impoverished Polish immigrant. At the age of 10, he developed scarlet fever, and lost a significant portion of his hearing, an ailment that isolated him from his peers. By the age of 14, he had been suspended from school, having acquired only a few brief years of formal education.

But the young man had a thirst for learning. His father arranged for him to visit Moscow when Tsiolkovsky was 16, where he took advantage of the freely available Chertkovskaya Library. He studied mathematics, physics, chemistry and mechanics, and he also stumbled onto the works of science fiction writer Jules Verne , whose novels on space travel inspired him. Tsiolkovsky calculated that Verne's method of using a giant cannon to fire a spacecraft to the moon, utilized in his novel "From the Earth to the Moon," would generate acceleration forces that would kill its passengers.

Tsiolkovsky returned home after three years in Moscow, eventually taking the exam to qualify him as a teacher. Before taking his first teaching job, he built a centrifuge with the idea of testing gravitational effects. Local chickens served as his test subjects.

He taught arithmetic and geometry in the local school in Borokvsk, a small town 70 miles south of Moscow. There, he married Varvara Sokolova and raised a family. In 1892, Tsiolkovsky was promoted to another teaching position in Kaluga, where he would remain until his death in 1935.

Pioneering work

Soon after his return home, Tsiolkovsky tried his hand at writing science fiction. However, he found himself focusing on the concrete problems that space travelers would have to deal with, such as the struggle to control a rocket as it traveled through gravitational fields. In 1883, he published an article about living in outer space that dealt with the effects of zero gravity .

Isolated, Tsiolkovsky found it difficult to stay abreast of new research. When he sought to publish his findings on the kinetic properties of gases, he was told that someone else had already published similar findings a quarter decade earlier.

Undaunted, Tsiolkovsky turned his eyes toward flight. He began to design airships, publishing his first work on the subject in 1892 and developing Russia's first wind tunnel . An 1894 article proposed the idea of a fully metal aircraft, and in 1895, he turned his eyes toward settling space .

In 1903, his manuscript "Exploration of the World Space with Reaction Machines" was published in Nauchnoe Obozrenie (Scientific Review) magazine. This and his follow-up articles are regarded as the world's first scientifically viable proposals to explore outer space with rockets. Tsiolkovsky's rockets were fueled by a mixture of liquid hydrogen and liquid oxygen, the same mix used on the space shuttle , though hydrogen had only been liquefied for the first time in 1898.

His manuscript included the equation now named for the scientist. Tsiolkovsky's formula provides the mathematical relationship between the changing mass of a rocket as it burns through fuel, the velocity of the exhaust gases, and the final speed of the rocket. It is considered a foundation of astronautics.

But though Tsiolkovsky was the first to delve into such complex problems, his role as a provincial schoolteacher, combined with the shutdown of the magazine, meant that very few copies of his research left Russia. In the 1920s, German scientist Hermann Oberthand American physicist Robert Goddard were independently reaching many of the same conclusions as Tsiolkovsky. Their separate parallel work set all three men as the "fathers of rocketry."

In 1929, Tsiolkovsky published another article elaborating on his thoughts on multistage rockets, which he described as required to allow a body to leave orbit. As each rocket consumed its fuel, it would break off from the main body.

Other ideas that Tsiolkovsky proposed including steering rockets in flight with graphite rudders, pumps to drive fuel from storage tanks to the combustion chamber, and propellants to cool parts of the rocket. He predicted the need for pressurized suits when astronauts left their spacecraft.

In Russia, Tsiolkovsky is known as "the father of theoretical and applied cosmonautics." His work helped drive the Russian space race, inspiring rocket designers such as Valentin Glushko and Sergey Korolyov. The most prominent crater on the far side of the moon bears his name, as does asteroid 1590 Tsiolkovsky.

Tsiolkovsky died at home on Sept. 19, 1935 at the age of 78.

Quotes by Tsiolkovsky

"The Earth is the cradle of mankind, but mankind cannot stay in the cradle forever."

"I do not remember how it got into my head to make the first calculations related to rocket. It seems to me the first seeds were planted by famous fantaseour, J. Verne."

"First, inevitably, the idea, the fantasy, the fairy tale. Then, scientific calculation. Ultimately, fulfillment crowns the dream."

"All the Universe is full of the life of perfect creatures."

"Mankind will not forever remain on Earth, but in the pursuit of light and space will first timidly emerge from the bounds of the atmosphere, and then advance until he has conquered the whole of circumsolar space."

"From the moment of using rocket devices a great new era will begin in astronomy: the epoch of the more intensive study of the firmament."

"My entire life consisted of musings, calculations, practical works, and trials. Many questions remain unanswered; many works are incomplete or unpublished. The most important things still lie ahead."

— Nola Taylor Redd, SPACE.com Contributor

Further reading:

• NASA's biography on Tsiolkovsky

Join our Space Forums to keep talking space on the latest missions, night sky and more! And if you have a news tip, correction or comment, let us know at: [email protected].

Get the Space.com Newsletter

Breaking space news, the latest updates on rocket launches, skywatching events and more!

Nola Taylor Tillman is a contributing writer for Space.com. She loves all things space and astronomy-related, and enjoys the opportunity to learn more. She has a Bachelor’s degree in English and Astrophysics from Agnes Scott college and served as an intern at Sky & Telescope magazine. In her free time, she homeschools her four children. Follow her on Twitter at @NolaTRedd

Science and music festival Starmus VII is about to rock Bratislava with a stellar lineup

China's Chang'e 6 mission to collect samples of the far side of the moon enters lunar orbit (video)

Blue Origin launches 1st crewed spaceflight since August 2022 (video)

Most Popular

• 2 'Star Wars: The Phantom Menace' at 25: Who are the angels on the moons of Iego?
• 3 Everything we know about 'A Quiet Place: Day One'
• 4 Bright green fireball lights up the skies over Portugal and Spain (photos)
• 5 Why a giant 'cold spot' in the cosmic microwave background has long perplexed astronomers